
一次関数をできるようになるためには「変化の割合」をしっかり理解することが大切なんだよね。だから今回は関数を学ぶ上でとっても大切な「変化の割合」について分かりやすく説明します。
1. 変化の割合とは
変化の割合の意味は \(x\)が1増加したときの \(y\)の増加量のことです。
まず公式を覚えちゃおう!
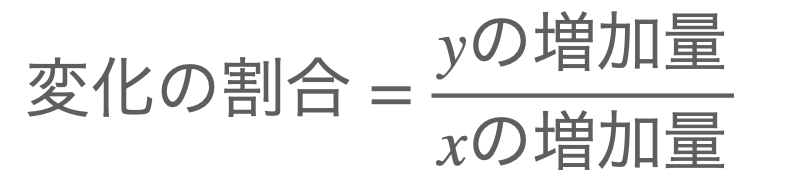
要は\(y\)の増加量を\(x\)の増加量で割り算すれば求められるってこと。
だから、変化の割合を求めるためには「\(\x\)の増加量」と「\(y\)の増加量」が分かればいいんだ。
例題
1.\(x\)の増加量が3で\(y\)の増加量が12のときの変化の割合は?
答:\(\LARGE \frac{12}{4}=3\)
2.\(x\)の増加量が4で\(y\)の増加量が8のときの変化の割合は?
答:\(\LARGE \frac{4}{8}=\frac{1}{2}\)
2. 一次関数の変化の割合
この変化の割合は色々な関数の問題でも出てくるんだけど、一次関数の場合は特徴があります。
それは、一次関数の変化の割合は常に一定ということです。どこの値をとって計算しても答が同じになるんですよ。
例えば、下の表の場合
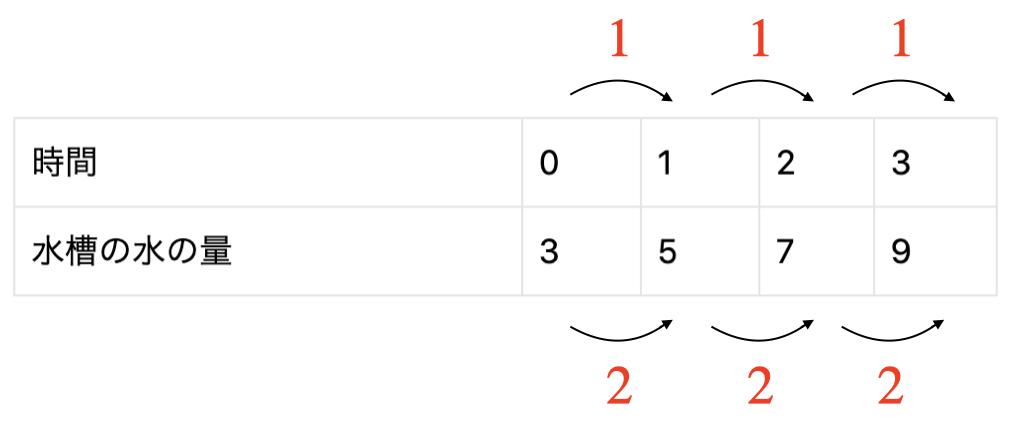
どこをとっても\(x\)が1増えるとき\(y\)は2ずつ増えてますよね。
これが一次関数の変化の割合の特徴です。
一次関数の一般式を覚えていますか?
\(y=ax+b\)でしたね。
この式の\(a\)の部分が変化の割合でした。
だから\(y=3x+5\)の場合は、変化の割合は3ですね。この関数は\(x\)が1増えると\(y\)が3ずつ増えていくのです。
変化の割合は常に一定である。
覚えておきましょう!
例題
一次関数\(y=2x-3\)の変化の割合は?
答:3
一次関数\(y=\frac{2}{3}x+5\)の変化の割合は?
答:\(\frac{2}{3}\)
3. 2点から変化の割合を出す方法
点\(( 3, 5)\)から点\(( 7 , 13)\)に変化するときの変化の割合は?
上の問題のように2つの座標から変化の割合を出す方法を伝授します。

座標を2つ並べて書きます。
左の\(x\)座標から右の\(x\)座標に向けて矢印を書きます。
右の座標から左の座標を引き算すれば、それが\(x\)の増加量になります。
同じように\(y\)座標もやってみましょう。
変化の割合の公式は、
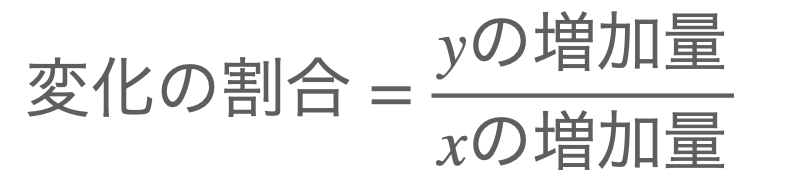
\(\frac{8}{4}=2\)
よって変化の割合は2になります。
\(x\)の増加量を下に、\(y\)の増加量を上に書くと計算ミスが減ります。
例題
点\(( 2, 1)\)から点\(( 7 , 21)\)に変化するときの変化の割合は?
答:\(\frac{21-1}{7-2}=\frac{20}{5}=4\)
点\(( -3, 2)\)から点\(( 7 , 12)\)に変化するときの変化の割合は?
答:\(\frac{12-2}{7-(-3)}=\frac{10}{10}=1\)
点\(( -10, 6)\)から点\(( -4 , -12)\)に変化するときの変化の割合は?
答:\(\frac{-12-6}{-4-(-10)}=\frac{-18}{6}=-3\)
点\(( 2, 1)\)から点\(( 6 , 3)\)に変化するときの変化の割合は?
答:\(\frac{3-1}{6-2}=\frac{2}{4}=-\frac{1}{2}\)
4.意外と質問が多い\(y\)の増加量の求め方
一次関数の変化の割合を指導しているときに意外と多い質問が、\(y\)の増加量の求め方です。
表があったり、2点が分かっていれば引き算するだけなのですが、式が与えられていて2点が分かっていない問題の時に質問が多いですね。例えば、
一次関数\(y=2x+4\)で、\(x\)が4増えるときの\(y\)の増加量を求めなさい。みたいな問題の時です。
この場合は、変化の割合の公式を変形します。
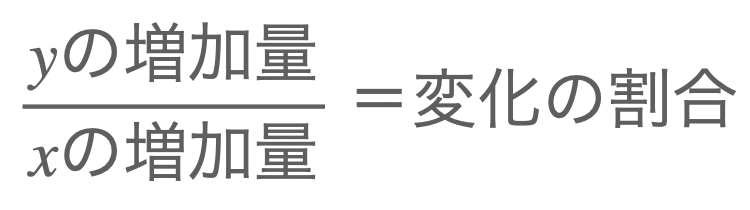
この公式の両辺に\(x\)の増加量を掛け算して、
\(y\)の増加量=変化の割合✖️\(x\)の増加量
に変形します。
要は、変化の割合に\(x\)の増加量を掛け算すれば、\(y\)の増加量が求めらるわけです。
だから上の問題の場合、変化の割合は2で\(x\)の増加量は4ですから\(2 \times 4=8\)と求めればいいのです。
例題
一次関数\(y=3x+12\)で、\(x\)の増加量が5の時の\(y\)の増加量を求めなさい。
答:\(3 \times 5=15\)
一次関数\(y=-\frac{2}{3}x-5\)で、\(x\)の増加量が12の時の\(y\)の増加量を求めなさい。
答:\(-\frac{2}{3} \times 12=-2 \times 4=-8\)
5. まとめ
理解できましたか?
理解できたら、後は学校の教科書や問題集で練習しましょうね。
「分かった」と「出来る」は違います。
「分かった」問題を「出来る」まで練習することで得点力がつきます。
頑張って下さいね^^
