今回は一次関数の直線の式の求め方について説明します。
一次関数の問題は直線の式が求めることができれば、ほぼ解決します。
できるようになれば苦手から得意にも変わることができますよ。頑張ってマスターしてくださいね。
一次関数実践編1:直線の式の求め方
一次関数の一般式は
\[y=ax+b\]
ですね。
直線の式を求める問題はこの一般式の \(a\) と\(b\) がいくつになるのかを計算して求めればいいわけです。
ですからまず一次関数の一般式における \(a\) と\(b\) の名前と意味を頭に入れておきましょう。

テストに出題されるパターンを簡単な順に紹介します。
出題例その1:\(a,b\)の2つともわかっている問題
いちばん簡単なパターンです。次のような問題です。
例題:次の条件を満たす直線の式を求めなさい。
(1) 変化の割合が \(2\) で切片が \(-3\)
一次関数の一般式の\(a,b\)の名前を覚えていればあとはこの数字を式に当てはめること(代入)で答えになります。
変化の割合は \(a\) で 切片は \(b\) ですから、答えは
\[y=2x-3\]
になります。
(2) 傾きが \(\displaystyle-\frac{2}{3}\)で切片が \(5\)
(1)と同じように代入して求めます。
\[ y=-\frac{2}{3}x+5 \]
この問題ができない場合は、まず上にある一般式の図を覚えましょう。
特に \(a \)は変化の割合と傾きの \(2 \)つの呼び方があるのでしっかり覚えてください。
出題例その3: \(a,b \)のどちらかがわかっている問題
このパターンは \(a,b \)のどちらかがわかっている場合です。
例題:次の条件を満たす直線の式を求めなさい。
(1) 変化の割合が\(3\)で、点\((2,-3)\)を通る直線
問題文から変化の割合\(3\) だと分かるよね。よって\(a=3\)です。
次に\(b\)を求めます。
\(a=3\)を一般式\(y=ax+b\)に代入すると、
\[y=3x+b\]
になるよね。
ここに、もう一つの条件である\((2,-3)\) を代入すると
\[-3=3\times 2+b\]
これを\(b\)の一次方程式として解くと
\[b=-9\]
よって、
\[y=3x-9\]
が答えになる。
(2)傾きが\(-2\)で、点\((-3,5)\)を通る直線
問題文から傾きが\(-2\) がわかるので、\(a=-2\)です。
(1)と同じように、
\(a=-2\)を一般式\(y=ax+b\)に代入すると、
\[y=-2x+b\]
になるよね。
ここに、もう一つの条件である\((-3,5)\) を代入すると
\[5=-2\times (-3)+b\]
これを\(b\)の一次方程式として解くと
\[b=-1\]
よって、
\[y=-2x-1\]
が答えです。
(3)切片が\(−3\)で、点\((2,5)\)を通る直線
今度は切片がわかっている場合。
問題文から切片は\(-3\)と分かるから、\(b=-3\)
これを一般式\(y=ax+b\)に代入すると、
\[y=ax-3\]
になる。
ここにもう一つの条件\((2,5)\)を代入する。
\[5=a\times 2-3\]
これを\(a\)の一次方程式として解くと
\[a=4\]
よって、
\[y=4x-3\]
が答え。
出題例その4:\(a,b\)の意味から考える問題
例題:次の条件を満たす直線の式を求めなさい。
(1) \(x\)が\(3\)増加するとき\(y\)が\(12\)増加し、点\((-5,10)\)を通る直線
この問題は変化の割合の意味が分かっていないと解けません。
変化の割合とは、\(x\)が1増加したときの\(y\)の増加量のことでしたね。
この問題では、\(x\)が3増加するとき\(y\)が12増加するので、\(x\)が1あたり増加するときの\(y\)の増加量は、
\[12 \div 3=4\]
\(4\)になる。
よって\(a=4\)が分かる。
後は上の例題と同じやり方で解けます。
\(a=4\)を一般式\(y=ax+b\)に代入すると、
\[y=4x+b\]
になるよね。
ここに、もう一つの条件である\((-5,10)\) を代入すると
\[10=4\times (-5)+b\]
これを\(b\)の一次方程式として解くと
\[b=30\]
よって、
\[y=4x+30\]
が答え。
(2)傾きが\(3\)で、\(x=0\)のとき\(y=-4\)の直線
\(x=0\)のとき\(y=-4\)から\(b\)が\(-4\)だと分かる。
なぜかというと、切片\(b\)の意味は\(x\)が0のときの\(y\)の値のことだからだ。
だからこの問題は言い換えると、
「傾きが\(3\)で、切片が\(-4\)である直線の式を求めなさい」になるから、
\(a=3\)と\(b=-4\)を一般式\(y=ax+b\)に代入して、
\[y=3x-4\]
が答えになるんだ。
*\(x=0\)のとき\(y=-4\)ということは\((0,-4)\)と同じだということも押さえておこう。
出題例その4:\(2\)点から直線の式を求める問題
\(2\)点から直線の式を求める問題は2通りのやり方があるので、あなたのやりやすい方で解きましょう。
1.連立方程式を立てて解く方法
教科書だとこっちがメインで解き方が載っている場合が多い。
要は、一般式\(y=ax+b\)にそれぞれの座標を代入して\(a,\ b\) の連立方程式として解けばいいのだ。例題(1)はこのやり方で解くね。
2.一次関数の意味を考えて解く方法
2点から変化の割合を求めてから、片方の座標を代入して解く方法。例題(2)はこのやり方で解きます。
例題:次の条件を満たす直線の式を求めなさい。
(1) \((-2 , \ 3)\) , \( \ \) \((6 , \ -1)\)
1.連立方程式で解く方法
まず\((-2 , \ 3)\)から。左が\(x\)座標、右が\(y\)座標なので、\(x=-2,\ y=3 \)になります。
これを一般式\(y=ax+b\)に代入すると、\(3=-2a+b\)になるので、左辺と右辺を入れ替えると、
\[-2a+b=3\]
同じように、\((6 , \ -1)\)も代入して
\[6a+b=-1\]
これらの2つの式を\(a,\ b\) の連立方程式として解けば良いわけです。
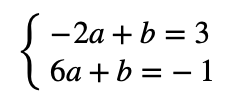
\(b\)の係数が1で揃っているので、上の式から下の式を引き算すれば\(a\)が求められますね。
\(a =\displaystyle-\frac{1}{2} \)
これを上下どちらかに代入すれば、\(b=2\)が求められます。
よって、答えは
\[ y=-\frac{1}{2}x+2 \]
となります。
(2) \(x=2のときy =3\), \( \ \) \(x =-1のときy =-9である。\)
2.一次関数の意味を考えて解く方法
まず変化の割合を求めます。
変化の割合は、\(y\)の増加量を\(x\)の増加量で割り算すれば求められましたね。
この例題の場合、\(x=2\)から\(x=-1\)に変化していると考えます。
\(3\)減ってますよね。これを言い換えると「\(-3\)増加している」になります。
\(y\)は\(3\)から\(-9\)に\(12\)減ってますよね。これは「\(-12\)増加している」と捉えます。
よって、変化の割合は
\[-12 \div (-3)=4\]
になります。
\(a=4\)が分かったので、ここから\(b\)を求めます。
ここからは上の例題と同じ計算になります。
まず、一般式\(y=ax+b\)に\(a=4\)を代入します。\(y=4x+b\)になりますね。
次にこの\(y=4x+b\)の式に、(x=2のときy =3), ( \ ) (x =-1のときy =-9)どちらかの条件を代入して\(b\)を求めてください。
そのときのコツは計算が楽になりそうな方を選ぶことです。今回は(x=2のときy =3)の方が楽そうなのでこれを代入して計算します。
\[3=4 \times 2+b\]
この式から、\(b=-5\)が求められます。
よって答えは、
\[y=4x-5\]
になります。
まとめ 一次関数実践編1:直線の式の求め方
まずは一般式を覚えましょう。

そして変化の割合(傾き)と切片の意味を理解して、問題を解くときにどのように使うのかを意識しましょう。
あとは教科書や学校のワークなど問題をある程度の数を解いて慣れていきましょう。
勉強は、結局のところ慣れなので。
解き方を理解てして、慣れるまで繰り返して解くこと。
これがコツになります。
