はじめに

「一次関数ってマジで意味わかんない!」
昨年、新入会の生徒から言われた言葉。
彼女は二学期の中間テストでやらかしてしまっての入塾でした。
数学はもともと嫌いで苦手な教科。特に一次関数に入ってからますます分からなくなったそうです。
そして、中間テストで今まで取ったことのない最低得点を取ってしまいました。
でも、その女子生徒は1年経った今「二次関数の応用問題」を解いてます。数学の成績も徐々に上がってます。
なぜその生徒は「一次関数ってマジで意味わかんない!」から「二次関数の応用問題」を解けるように変化したのでしょうか?
その理由を今回お話します。
この記事を読むといい人
- 一次関数で困っている人
- 一次関数ができるようになりたい人
- 問題を解く際に時間がかかるのでもっと速く問題を解けるようになりたい人
- 学校のテストをなんとかしたい人
- 数学を学ぶ際にとても重要な「抽象化」と「具体化」を学びたい人
これに当てはまる人は読んでみてください。
※そもそも「関数」ってなんなのかさっぱり分からない場合はこちらの記事↓を読んでから、この記事を読むと理解がさらに深まります。
これで一次関数は怖くない!中学生のための関数超入門ガイド
なぜ一次関数が苦手な人が多いのか?
私が思うに理由は2つあります。保護者説明会で話していた内容です。
- 一次関数から「抽象化」など数学的な要素が増えるから
- 反抗期に入りやすい中学2年生の夏頃に授業が行われるから
一次関数から数学を学ぶにあたり大切な「抽象化」の考えが必要になってくるので、今までよりも集中して取り組まないといけないのに、ちょうど反抗期に入りやすい時期に学習するので苦手な人が多くなると言うことです。
中学2年生の夏の頃って大人のことうざくなってくるし、高校受験まではまだ先だし。部活も3年生が引退するとメインになってきて練習もハードになるし。
勉強したく無くなることがどんどん増えてきます。
もちろん将来見据えてしっかり勉強できる人はいます。精神年齢が高い人や将来の夢があってそのために頑張っている人です。
ですが、13歳-14歳の頃にすでに夢があって目標に向かって突き進んでいる人ってまだまだ少ないです。
目標が無いのに勉強なんてできないですよね。それだったらYouTubeで動画を見たりゲームやったりしていたいし。
だから勉強する気にならない、やっても集中してないことが多くなるんですよね。実際、私も中学2年生の頃は勉強やってなかったもの。
しかも内容は難しくなるから、なおさらやる気なくなるし。
そんなわけで、一次関数が苦手な人が多いのです。
一次関数ができるようになるための3つのコツ
ではどうすればいいのか?って話に入ります。
実は一次関数ができるようになるにはコツがあるんですよ。そのコツを意識して勉強するのかしないのかで結果が変わるんです。
一次関数ができるようになるための時間も短くなるし、この後の数学の勉強の仕方も変わるので数学が得意になる可能性すら出てくるんですね。
そのコツには3つあります。
一次関数ができるようになるための3つのコツ
- 抽象化を意識する
- 増加量(変化量)と値(座標)の違いを頭に叩き込む
- 基本的なパターン(バッテン代入など)を習得する
この3つです。
えっ!?「いきなり難しそう」
大丈夫です。ゆっくり分かりやすく説明しますね。
1.抽象化を意識する
抽象化ってWIKIで調べると「思考における手法のひとつで、対象から注目すべき要素を重点的に抜き出して他は捨て去る方法である」と書いてあります。
分かりやすく言うと、具体的な小さなことがらからもっと大きな概念に置き換えることです。
えっ!?何言ってるのか分からない。確かにこんな説明では分からないですよね、具体的に説明します。
抽象化の具体例1
まずはこの動画に出てくる短足マンチカンのプリンちゃん可愛いですよね。とっても可愛いので、最近よく見て癒されています笑。
この短足マンチカンのプリンちゃんを「抽象化」していきます。
まず、この「短足マンチカンのプリン」ちゃんは世界で唯一1匹ですよね。
少し抽象度を上げると、「茶トラの短足マンチカン」になります。
さらに上げると「茶トラの猫」になり、
どんどん抽象化していくと「猫」→「ほ乳類」→「脊椎動物」→「動物」→「生き物」
もうプリンちゃんはだけではなくなりました。探すのも大変そうです。
このように大きな概念に置き換えることを抽象化といいます。
抽象化の具体例2
数学の場合の抽象化はどうすればいいでしょうか?
数学では、具体的なことがらから表やグラフなどを作成していきます。
そして表やグラフから規則などを見つけていきます。そこからさらに公式を導いたりしていくことを抽象化というんですね。
具体的に説明します。
・例えば、いま水槽に3リットルの水が入っていて、そこに毎分2リットルずつ水を入れていくとします。この具体例を抽象化してみましょう。
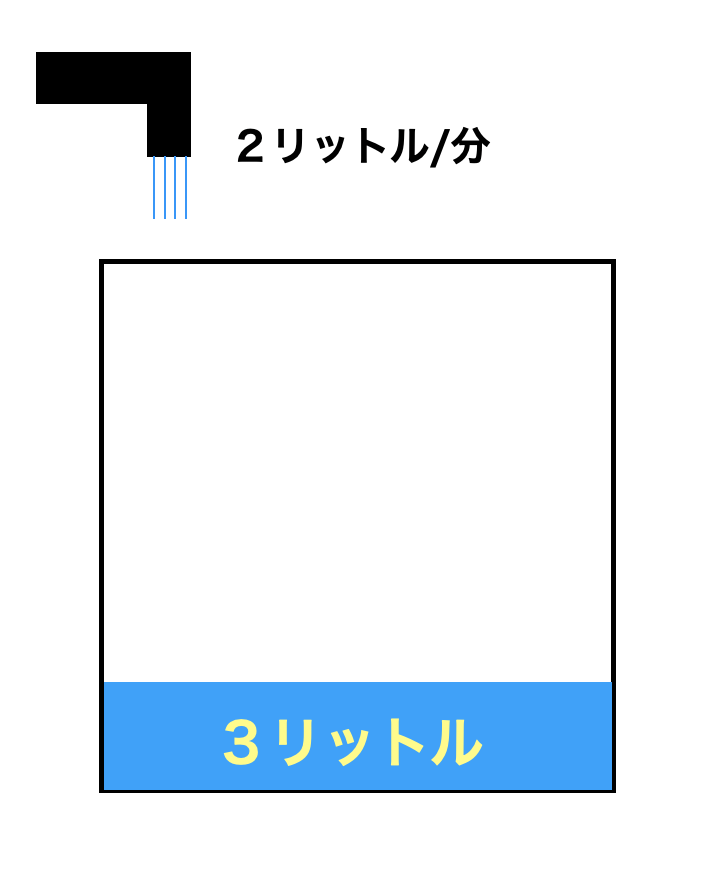
左の図にあるように、すでに3リットル水は入っています。
ここに、毎分2リットルずつ水を入れていくわけです。
そうすると、1分後には5リットル、2分後には7リットルと水槽に水がたまっていきますよね。
その様子を表やグラフ化していきます。
| 時間 | 0 | 1 | 2 | 3 |
| 水槽の水の量 | 3 | 5 | 7 | 9 |
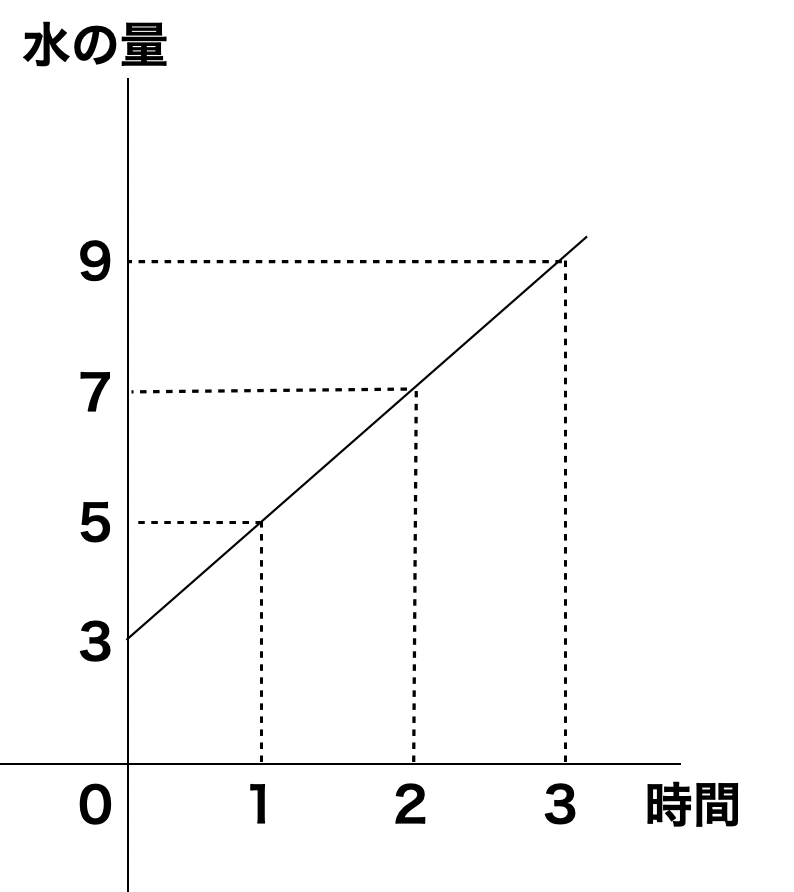
次はグラフ化します。
たて軸に水の量、よこ軸は時間です。
はじめは3リットルで、そこに1分あたり2リットルずつ入りますから左のような右上がりの直線のグラフになります。
右上がりは「増えている」ことを表しています。
直線なのは決まった時間に入る水の量が一定(同じ)ということを表しています。
もちろん、問題の意味からではなく、表からグラフを作ってもOKです。
はじめは、水と水槽の話でした。ところが変化していく量を表やグラフにしていくと、そこにはすでに水も水槽も関係なくなります。ただの数字と線が書いてあるだけです。
この方が余計なこと考えないので、規則を見つけるには分かりやすいんですね。
このように、問題から表やグラフにすることが「抽象化」の第一歩です。
上の例の場合、時間と水槽にたまる水の量は y=2x+3 という一次関数の関係が導かれるわけです。
1-2:一次関数の抽象化でもっとも大切なこと(最重要事項)
「抽象化はなんとなくわかったけど、それを一次関数の問題を解くときにどうやって取り入れていけばいいのかがよく分からない……」
ではどうすればいいのか?
次の図を暗記してください!!!

一次関数の鉄則の使い方
一次関数の問題を解くときに、つまづくポイントとして問題の種類がたくさんあるので覚えきれないというのがあります。頭の中で「この問題どうやって解くんだっけ?」とゴチャゴチャしちゃうんですね。
表の空欄をうめたり、増加量を求めたり、変化の割合を求めたり、式を求めたり、グラフをかいたり、点が動いたり、図形と絡んで出題されたり……、
これ1つ1つのパターンを覚えようするには、まず1つ1つのパターンの理解と演習が必要なります。
大変ですよね。
そこで、上の鉄則をもう一度見てください。
実はこの鉄則を覚えるだけでほとんどの問題が解けてしまうですよ!
要は色々な種類の問題があるけれど、一次関数の問題の解き方って結局この鉄則なんだよってこと。
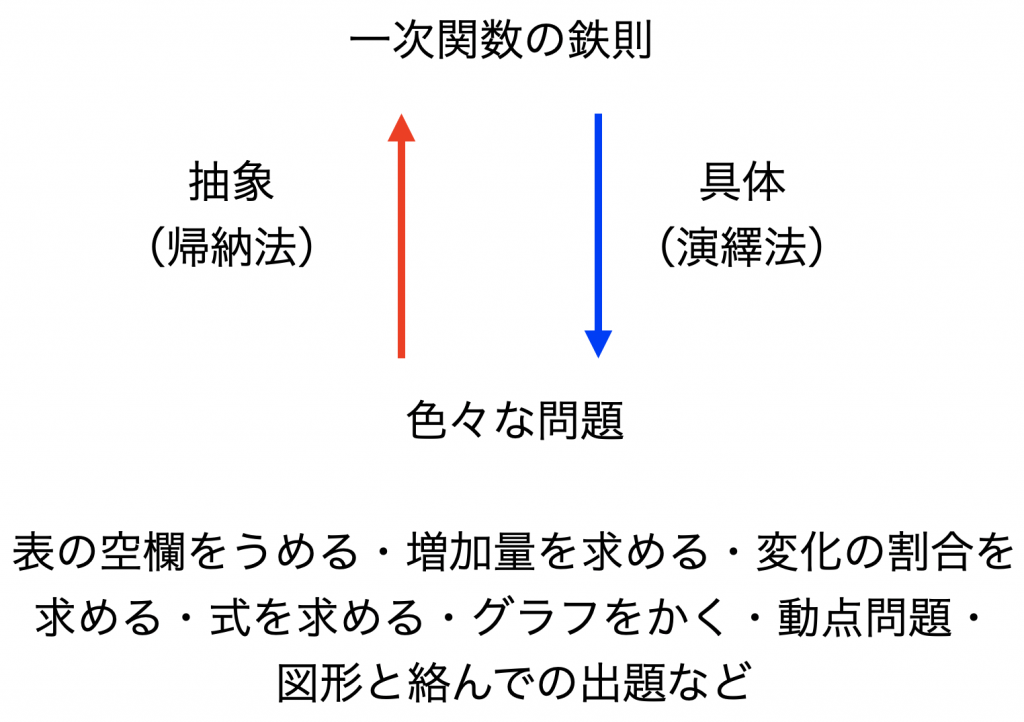
どんな問題があっても、結局のところまずは一次関数の一般式を求めることができればほぼ解決なわけですね。
ですから、それぞれの問題に対して鉄則の使い方がわかっていれば正直なところ鉄則を覚えていればほとんどの問題が解けてしまうということなんですよね。数学が得意な子供な無意識にそれが分かるので、サクサク解けてしまうんですよ。
ですから、一次関数が苦手ならまず鉄則を覚えてください。それから練習することであなたの一次関数を解く力は間違いなくアップするでしょう。
2.増加量(変化量)と値(座標)の違いを頭に叩き込む
私は一次関数を教えていて気をつけてることがあります。それは、増加量と値の違いをきっちりと教え込むことです。何度も確認します。それはしつこいくらい笑
なぜかというと、その違いがあいまいでできなくなるケースをたくさん見てきたからです。数学が得意な生徒や先生は頭がいいのでそんなこと当たり前じゃんって思っているようです。でもそこをしっかり教えない教師のクラスは一次関数が崩壊してるケースがよくあります。
次の表を見て増加量と値の違いを確認しましょう。
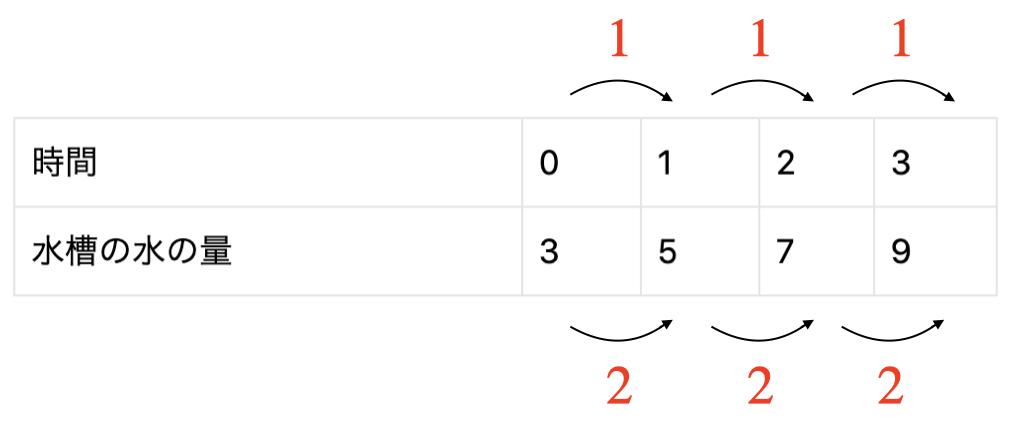
表の中にある黒い数字が値で、2つの数字の差にあたる赤い数字が増加量を表しています。
値は表や座標などで実際に書いてあるので確認しやすいですが、増加量は2数の引いた差なので目に見えないんですね。この2つを意識しながら問題を解くだけで正答率は高くなります。
基本的なパターン(バッテン代入など)を習得する
一次関数の式を求めるときに使う方法でバッテン代入と呼ばれている方法があります。
こんなのです。

こういういくつかよく使う方法はしっかり練習しましょう。一次関数は基本的に代入ができれば解けますから。
まとめ
一次関数について、「できるようになる3つのコツ」と題して書いてきました。少しレベルが高いと思った人もいるかもしれませんが、騙されたと思って、
- 抽象化を意識する
- 増加量(変化量)と値(座標)の違いを頭に叩き込む
- 基本的なパターン(バッテン代入など)を習得する
を意識しながら解いて見て下さい。必ず結果は変わりますから。
一次関数のそれぞれの解き方については、パターン別にどんどん書いていきますのでお楽しみに。
さて、まずは学校の宿題やワークをやってみましょう。もちろん鉄則を意識して下さいね。
