今回は「一次関数のグラフ書き」のテストで高得点を取るための攻略法がテーマです。
コツをつかんでしまえば早く書けるようになりますからマスターして下さいませ。
では、行ってみましょう!
一次関数のグラフ書き方の手順
まず一次関数のグラフ書きです。
一次関数のグラフってこんな直線でしたね。

直線を書くには2点が取れれば書けます。
ですから、テストで時間をかけずにグラフを書くには「いかに早く2点を見つけること」が必要です。
一次関数のグラフの書き方:2点をすばやく見つけるためのコツ
例えば、\(y=2x+3\)のグラフ
変化の割合(傾き)が2で切片が3です。この傾きと切片の2つを押さえます。
そして、切片がスタート地点になります。この場合は3が1つ目の点(スタートの点)になります。
2点目の見つけ方
そして、変化の割合に注目します。
変化の割合とは、
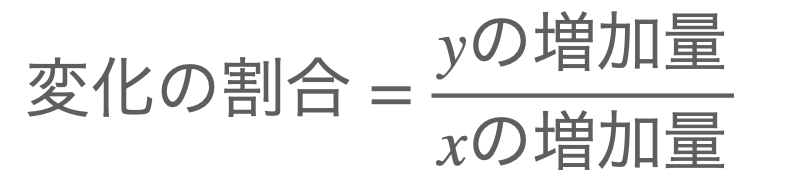
でしたね。
ですから、変化の割合が2ということは、
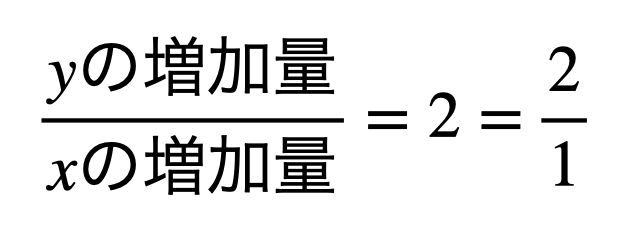
この分母と分子に同じ数をかけていくと
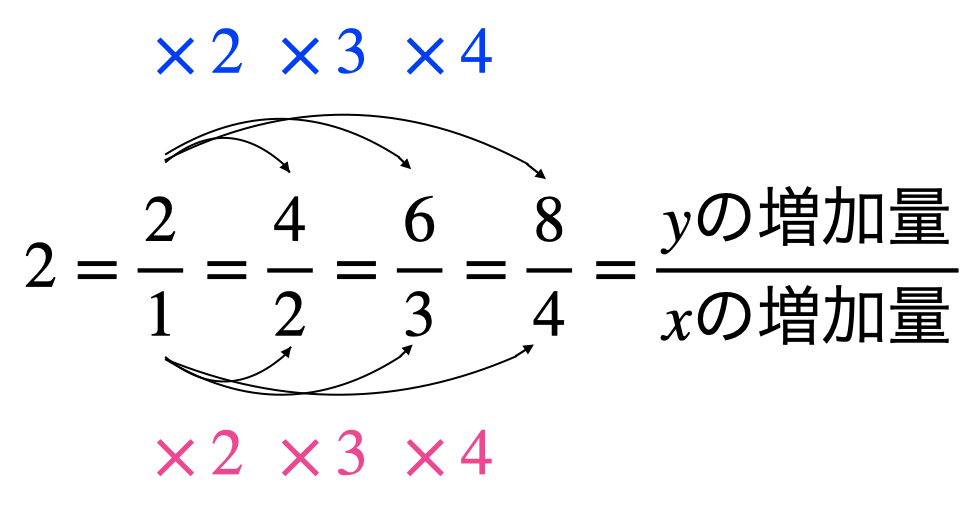
になります。
これを図で表すとこんなイメージなります。
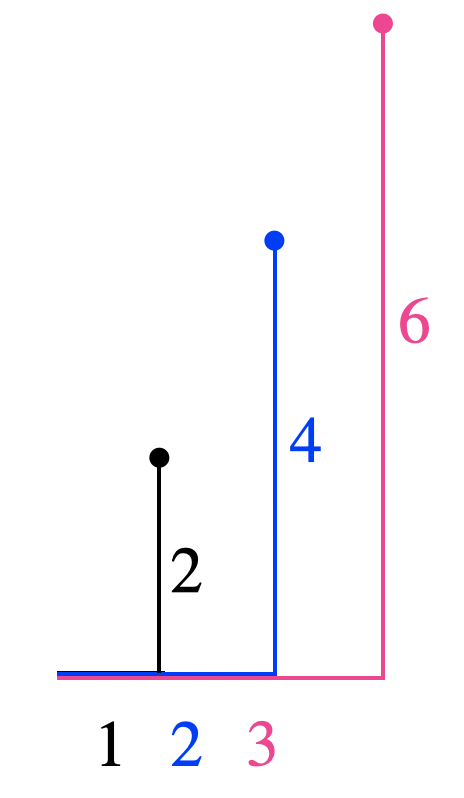
\(x\)の増加量は横の動き、\(y\)の増加量は縦の動きになります。
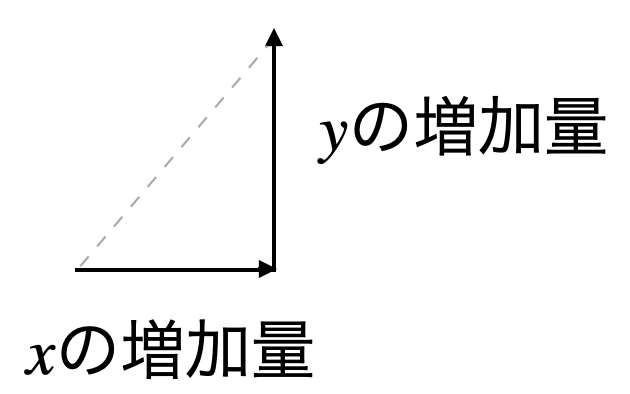
上のような変化の割合の三角形のイメージを頭に作って下さい。
まず、分母の数を横にとって、
次に、分子の数を縦に取ります。プラスの数なら上むき、マイナスなら下向きです。
例えば、変化の割合(傾き)が 3ならば、\(3=\frac{3}{1}\)のように 分数で考えて、変化の割合の三角形を作って2点目を決めます。

ただ、なるべく遠くに点を取って定規で線を引いた方がズレないので、2倍、3倍して\(\frac{6}{2}\)、\(\frac{9}{3}\)のように変化の割合の三角形を大きくして、2点目をはじめの点からなるべく離して取ると上手く書けます。
変化の割合(傾き)が分数の場合も同じです。
例えば、変化の割合(傾き)が\(\frac{2}{3}\)の場合、
右横に3行って上に2行ったところに2点目をクルクルっと取りましょう。
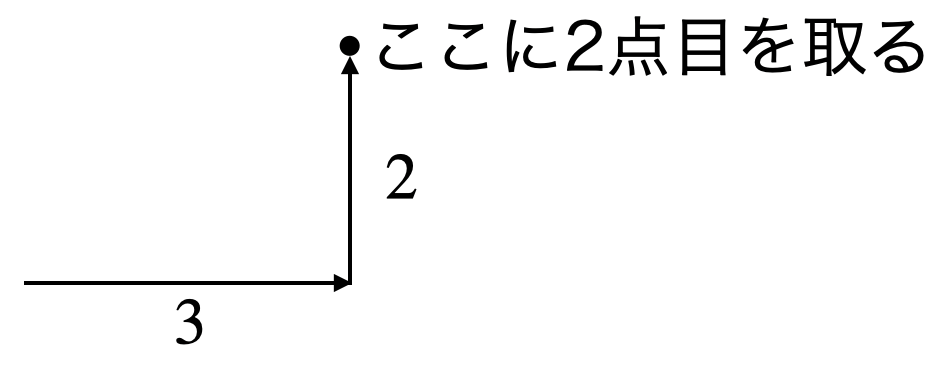
変化の割合(傾き)が負の数(マイナスの数)の場合
次に、変化の割合(傾き)が\(-\frac{2}{3}\)の場合です。
負の数の場合は、\(x\)の増加量は+で\(y\)の増加量は−で考えます。
この場合は\(x\)の増加量は+3、\(y\)の増加量は−2と考えます。
−の場合は下に矢印を書きます。
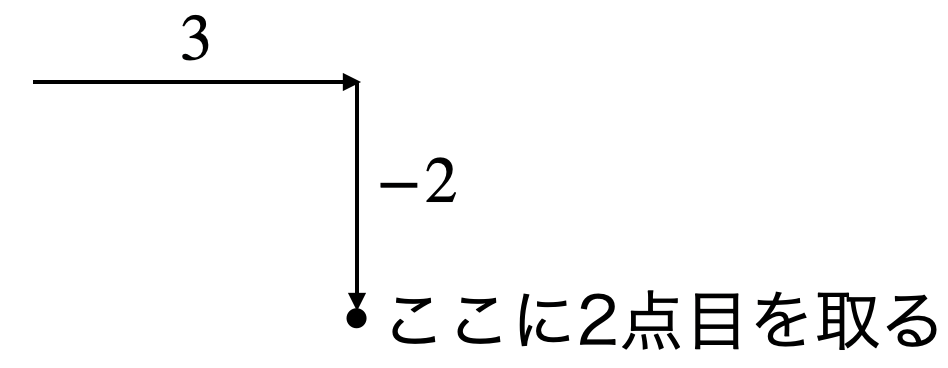
こんな感じです。
演習:\(y=\frac{3}{4}+2\)のグラフを書け
\(y\)軸上に切片の2を取ってグルグルっと丸く点をつけます
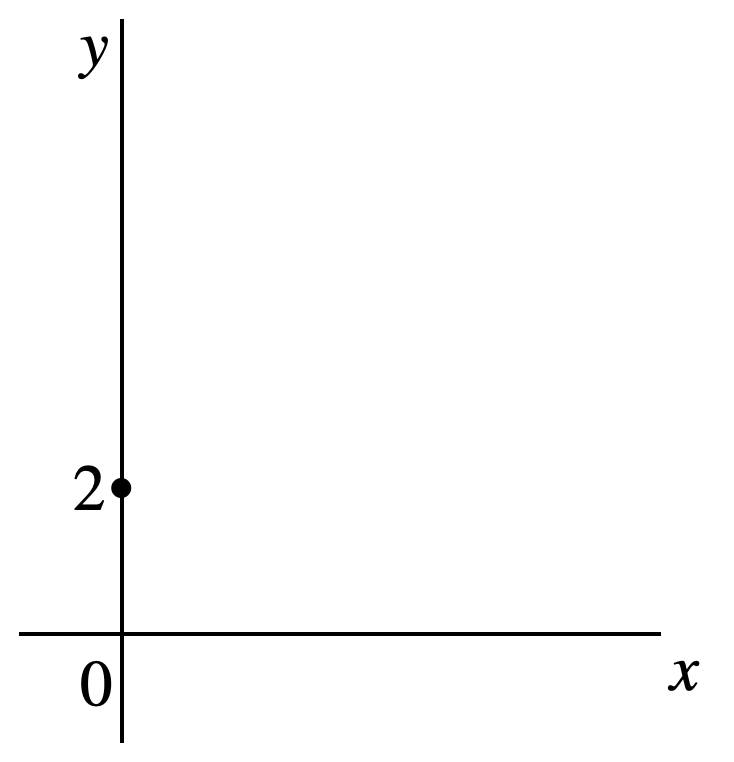
次に、変化の割合(傾き)の三角形を作ります。この場合は右横に4行って、上に3を取ります。
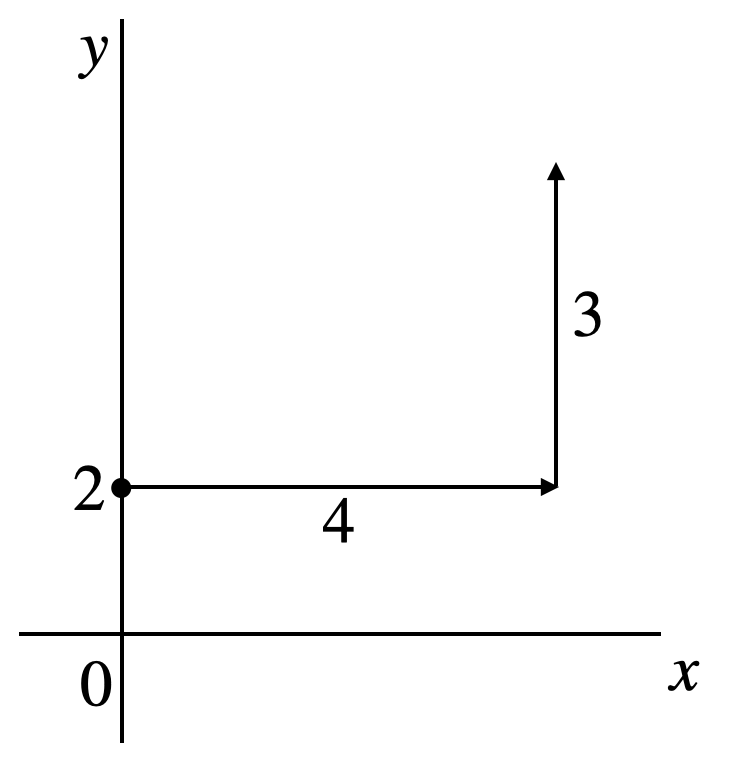
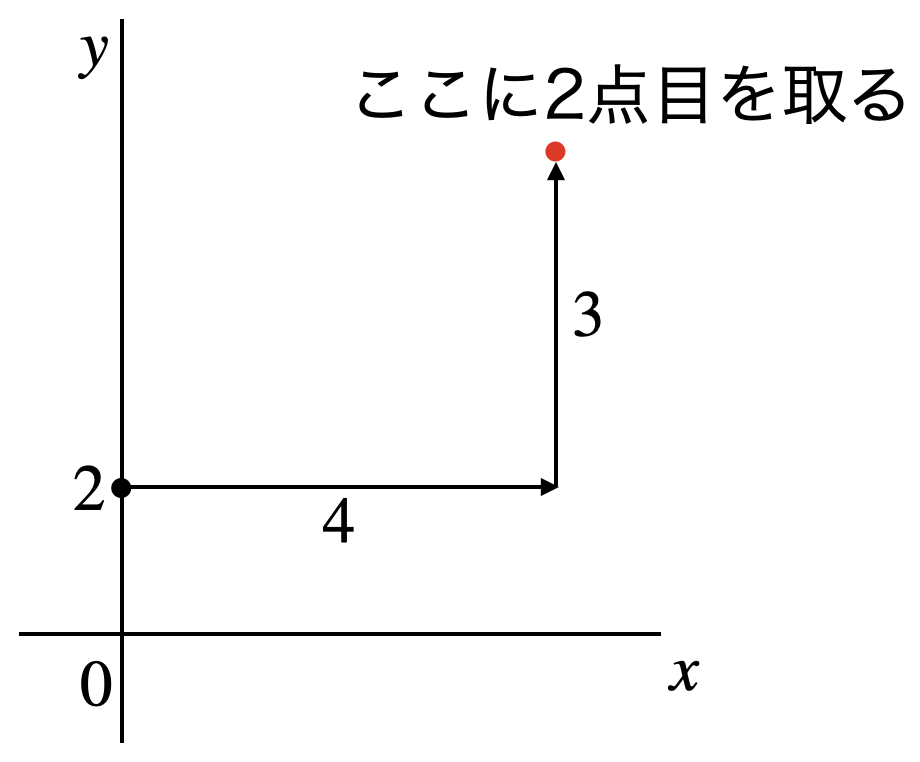
この2つの点を定規で結びます。
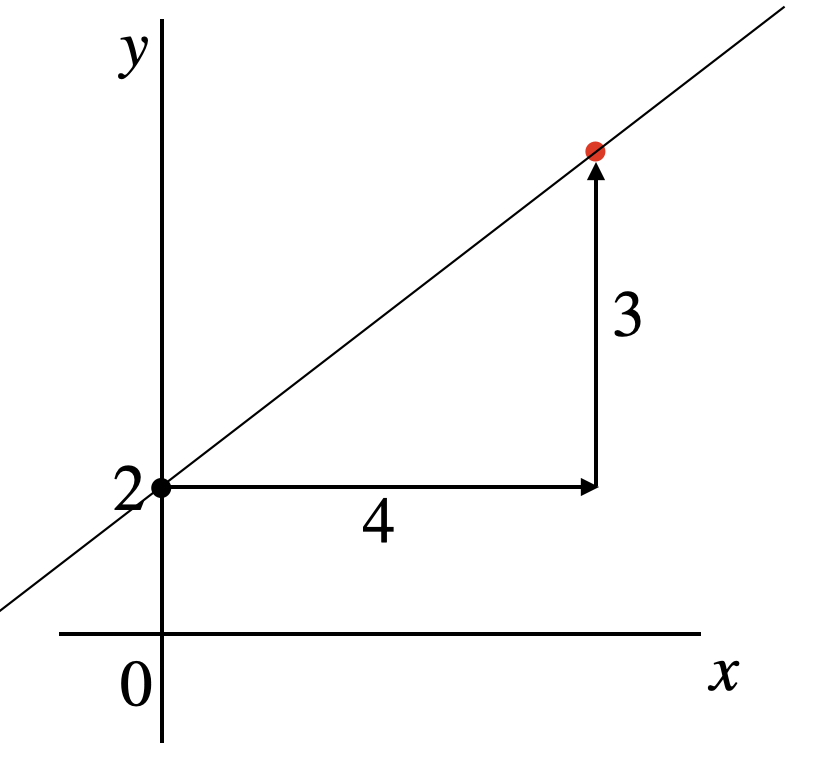
完成!!お疲れさま^^
一次関数のグラフの書き方:まとめ
- 1点目は切片になる
- 変化の割合(傾き)の三角形を作って2点目を見つける
- 定規で直線に結ぶ
細かいポイント
- 直線はグラフ用紙の端から端まできちんと書きましょう
- グラフの横に問題番号やグラフの式を書きましょう
- 2点を取るときはなるべく離れている2点を結んだ方が綺麗な直線が書けます
勉強なんて慣れだから、1回でうまくいかなくても何回か練習すれば必ずうまく書けるようになりますよ!
頑張ってね^^
