1. え?関数って何?【中学生向け超基礎解説】
「関数って何だか難しそう…」「グラフとか記号がいっぱいで、もうイヤ!」
そんな風に思っている中学生の皆さん、こんにちは!
実は、関数は決して怖いものではありません。このガイドを読めば、関数の基本的な考え方から、グラフの読み解き方まで、スッキリと理解できるようになりますよ!
「これで関数は怖くない!」を合言葉に、一緒に一歩ずつ関数ワールドを探検してみましょう!
1-1. まずはイメージ!ブラックボックスで関数を体験
関数が苦手になる理由はいくつかありますが、一番大きいのは抽象の概念がもろに入ってくることです。
具体的な水槽の話から、数値の関係性を抽象化して表やグラフ、そして式を求めることから始まります。
その後にいきなり抽象化された数字だけの世界に放り込まれるので、抽象と具体の行ききを理解できないと「ここはどこ?」「私は誰?」状態になってしまい、関数ってわけわからん!?となるのです。
そこで、関数を理解するために関数とはこんなイメージなんだよってことを体験しましょう。
関数を理解するためによく使われる例えがブラックボックスです。
ここにブラックボックスがあります。

このブラックボックスの左側から入力して右側から出力します。

左側から色を入力して、ブラックボックスを通してある法則で右側から出力しました。このブラックボックスにはどんな法則があるか分かりますか?

そうです、「白を混ぜる」という法則ですね。
このように入力したものを「ある法則」に従って出力するものが関数なのです。
次はどんな法則で出力しているか分かりますか?
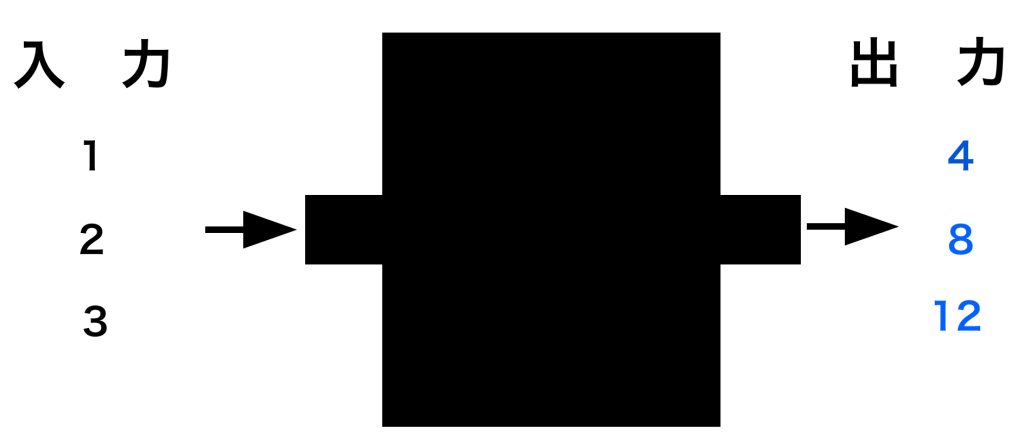
今度は入力した数を「4倍する法則」ですね。
関数では一般的に入力を \(x\) 、出力を \(y\) を使って表します。

上の図の関数を式で表すと、入力(\(x\))した数値を4倍した数が出力(\(y\))になるので、\(y=4x\) になるわけです。
ここで、\(x\) のことを独立変数、\(y\) のことを従属変数と言います。中学数学で変数という用語はさらっと紹介されます。簡単にいうと未知数のことです。
\(x\) のことを独立変数と呼ぶのは、\(x\) にはその関数の法則を抜きに(独立して)、どんな数字も当てはめることができるからです。
それに対して\(y\) のことを従属変数と呼ぶのは、その関数の法則に従って数が決まるからです。従属とは従ってという意味ですね。
詳しくは高校数学で学びます。
1-2. 大事なキーワード!「増加量」と「値」の違いをつかめ!
関数が苦手な人の特徴の1つに「増加量」と「値」の違いがよく分からず、ごっちゃになってしまっていることがあります。
「増加量」と「値」の違いをしっかり理解して使い分けることができると、途端に関数が得意になります。
増加量とは、その名の通り「増えている量」ですよね。
例えば、あなたは今3,000円持っているとします。お小遣いをもらって8,000円になりました。
この場合の増加量はいくらになりますか?
そうです、「5,000円」になりますよね。
この「5,000円」を計算で出すには8000-3000=5000と引き算で出します。
引き算の答えのことを「差」と言いますよね。
ですから増加量のことは「差」で求めるわけです。
それに対して「値」というのは\(x=3\)とか\(y=-2\)のように表せれます。
例えば、「\(x=3\)のとき\(y=-2\)で、\(x=7\)のとき\(y=10\)」の場合、
\(x\)は\(x=3\)から\(x=7\)になっているので、\(x\)の増加量は7-3=4になります。
\(y\)は\(y=-2\)から\(y=10\)になってます。ですから10-(-2)=10+(+2)=12になるわけです。
このように「増加量」と「値」というのは両方とも数字なのですが、意味が違います。
この違いをしっかり理解してそれぞれを求められるようになれば一次関数はすぐに得意になれますよ。
なぜかというと、一次関数で一番重要なのは「変化の割合」であり、「変化の割合」とはまさに\(x\)が1増加するときの\(y\)の増加量のことだからです。
「変化の割合」を求める公式は↓です。
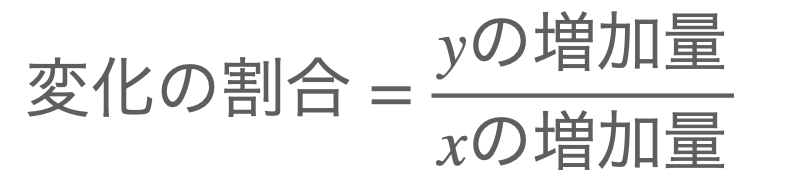
\(y\)の増加量を\(x\)の増加量で割れば求めることができます。
ですから、増加量とは差のことである。引き算をして求めるんだ!と意識して覚えてくださいね。
その上で練習問題を解いていけば、関数の問題はすらすら解けるようになりますから。
2. 関数を式で表してみよう!【中2数学の基本】
2-1. \(y = ax\) ってどんな意味?比例の関係
まずは中学1年生で習った「比例」について復習しましょう。
比例とは「\(x\) が2倍、3倍…、になる\(y\) も2倍、3倍…になる関係」のことでしたね。
比例の一般式は、\(y=ax\) でした。この\(a\)のことを比例定数といいました。
比例とは\(x\)に入力された数にこの比例定数を掛け算した「法則」のことです。
ですから、比例定数\(a\)を求めることができたら、比例の謎は解けたようなものなのです。
求め方は、公式\(a=\frac{y}{x}\)で求めてもいいですし、一般式\(y=ax\) の\(x\)と\(y\)に問題文で分かっている値を代入して求めてもOKです。
実はこの \(y=ax\) という比例も一次関数の仲間なんです。
\(y=ax\) は\(y=ax+b\)の\(b\) が\(0\) の場合を表しているんですね。
\(y\)切片が \(0\) だから原点を通るわけです。
2-2. \(y = \frac{a}{x}\) 反比例も簡単理解!
中学1年生のときに比例と一緒に習った反比例についても少し見ていきましょう。
反比例の一般式は、
\[y = \frac{a}{x}\]
でしたね。
\(x\) が2倍、3倍となると、 それに従って\(y\)は \(\frac{1}{2}\)倍、\(\frac{1}{3}\)になる関係のことを反比例と言いました。
反比例でもこの\(a\)のことを比例定数といいます。(※反比例定数とは言いません)
小学校のではこの\(a\)のことを「決まった数」と教えています。
ですから、反比例とはこの決まった数を\(x\)に入力した数で割り算する「法則」で出力\(y\)が決まります。
反比例は一次関数の仲間ではありません。
一次関数は \(y=ax+b\)という一次式で表される関数です。反比例は \(y = \frac{a}{x}\) なので、\(x\)が分母にあります。この場合は一次式とは言わないので一次関数ではありません。
また一次関数は変化の割合が一定な関数です。
例えば、\(y=2x+3\)という一次関数があります。この変化を表で表すと、

となります。
この表から\(x\)が\(1\)増加すると、それに従って\(y\)が\(2\)ずつ増加するのが読み取れますね。
このように一次関数は変化の割合が一定です。
今度は反比例を見てみましょう。
\(y = \frac{2}{x}\)という反比例を表で表します。
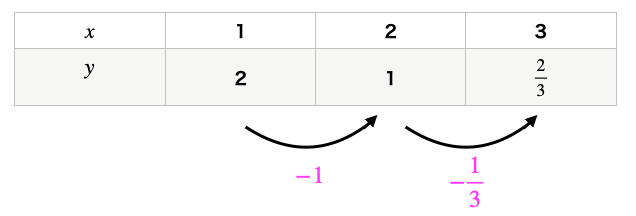
表のように、\(x\)の増加量が一定ではありませんね。ですから反比例は一次関数ではありません。
2-3. いろんな関数にチャレンジ!一次関数って?
では、中学2年生で習う「一次関数」についてみていきます。
一次関数は \(y=ax+b\)という一次式で表される関数です。
\(a\)のことを変化の割合(傾き)、\(b\)のことを切片(※\(y\)切片)と言います。
ではどんな法則なのか?
それは、\(x\)に入力した数を何倍(かけ算)してから、さらにある数を足し算する「法則」です。
入力した数にかけ算するのは\(a\)変化の割合で、その後に足し算するのは\(b\)の切片です。
例えば、\(y=2x+3\) と言う一次関数の場合、\(x\)に入力した数を \(2\) 倍してから\(+3\)を足す法則のことです。
\(y=-3x-5\)の場合は、 \(x\)に入力した数を \(-3\) 倍してから\(-5\)を足す法則になるわけです。
一次関数の法則は2回の計算があるので、難しい印象を持ってしまうのかもしれません。
ただ、これも慣れの問題なので適切な方法で繰り返し練習すればできるようになります。
そのときに気をつけて欲しいのは上の「1-2. 大事なキーワード!「増加量」と「値」の違いをつかめ!」のところなので繰り返し読んで、問題を解くときに意識してくださいね。
一次関数の解き方のコツはこちらの記事をお読みください。
3 関数のまとめ
関数とは入力と出力の関係のことでした。\(x\)に入力してある法則にしたがって\(y\)を出力する関係のことです。
\(x\)に入力した数を何倍かする「法則」を比例、比例定数(決まった数)を\(x\)に入力した数で割っていく「法則」を反比例と言います。
一次関数は、\(x\)に入力した数を何倍かした後にある数を足し算する「法則」でした。入力した数に\(a\)変化の割合を掛け算してから、切片の数を足し算して出力する関係のことです。
比例や反比例は1回の操作(計算)で終わるのに、一次関数は2回の操作(計算)があるので難しい印象がありますが、慣れれば簡単に求められるようになるので、諦めずにマスターしてくださいね。
