[mathjax]数学なんてまじで意味わかんないし、因数分解なんて出来なくたって将来困らないだろって思ってませんか。でも学校の定期テストあるからせめて平均点くらいは取っておかないとかっこ悪いし……。
今回はそんな数学が苦手なんだけで、なんとか定期テストで赤点を阻止したい人のために書きました。
因数分解が出来ないと、この後に出てくる二次方程式や二次関数が解けなくなるので実は大切なんですよ。もしあなたが中学生だったら入試で平均点は取れないです。むしろ数学が足かせになって志望校のランクダウンだってありうるし、高校生だったら留年!?嫌ですよね。だからこのサイトで因数分解の基本をマスターしてくださいね。
この記事を読むのがオススメな人
- 読むといい人:数学が苦手、だけど卒業するために宿題やテストをぎりなんとかしたい人。
- 読まない方がいい人:数学が得意で更なる上の数学力を求めている人には時間の無駄だから読まなくていいです。
- このページで因数分解の基本をマスターできるので計算力アップします。普段のミニテストや定期テストに向けて頑張っていきましょう。
そもそも因数分解ってなに?
因数とは?
因数分解を理解する前に、、そもそも「因数」って何よ?という話をします。
例えば、12。 掛け算に直すと、12=4×3 と表せますよね。
この掛け算に直したときの4と3を因数といいます。
簡単に言うと、掛け算に直した一つ一つの数や文字を因数と言うんですね。
因数分解とは?
因数分解とは、数や式を和や差の形から積(掛け算)の形に直すことをいいます。
$$x^2-5x+6=(x-2)(x-3)$$
みたいに和や差の式を積の式に変えることを因数分解というんですね。
因数分解の大鉄則中の大鉄則!
因数分解というと公式(乗法公式)ってイメージありますよね。でも、それ以前に大鉄則があるんですよ。鉄則中の鉄則が。それをまず伝授します。
因数分解の大鉄則とは!?
因数分解の大鉄則、それは…、「共通因数で括る」です!
$$ax+ay=a(x+y)$$とか
$$4ax-6ay=2a(2x-3y)みたいなやつです。
えっ!?それが大鉄則かよ〜!って思ったかもしれません。でもそのくらい「共通因数で括る」って重要なことなんですよ。それをついうっかり忘れてしまったがために、テストで点数を落とした子どもは多いです。このサイトを読んでくれたあなたにそうなって欲しくないので、注意してくださいね。
共通因数で括(くく)るとは?
では、共通因数とはなんなのか。次の式見てをください。
$$ax+bx$$
これは\(a×x+b×x\)なので、左の項の\(x\)と右の項の\(x\)が共通してますよね。
このように全部の項にある項のことを「共通因数」と言います。
この全部に項にある「共通因数」を式の先頭(1番左側ね)に持ってきてその後を()でくくるわけです。
ですから、因数分解の問題を解く時は必ず「共通因数」があるかないかを確認する癖をつけてくださいね。
因数分解で使う公式「乗法公式」はこうやって使う
共通因数を確認して共通因数でくくった、もしくは無かったと確認した。
その次にやることは公式を使います。式の展開で使った乗法公式を因数分解でも活用します。
要は式の展開の逆をやればいいんですね。
因数分解に入る前に、まずは4つの公式と使い方の復習から。
乗法公式の復習
乗法公式
- \((x+a)(x+b)=x^2+(a+b)x+ab\)
- \((a+b)^2=a^2+2ab+b^2\)
- \((a-b)^2=a^2-2ab+b^2\)
- \((a+b)(a-b)=a^2-b^2\)
それぞれ説明します。
\((x+a)(x+b)=x^2+(a+b)x+ab\)の使い方
\((x+2)(x+3)\)を展開するには、+2と+3を足した+5をxの前につけて、掛けた+6を定数項(数字だけの項)にします。
\(x^2+5x+6\)になればOKです!
覚える呪文は「足して、かける!」です。
\((a+b)^2=a^2+2ab+b^2\)の使い方
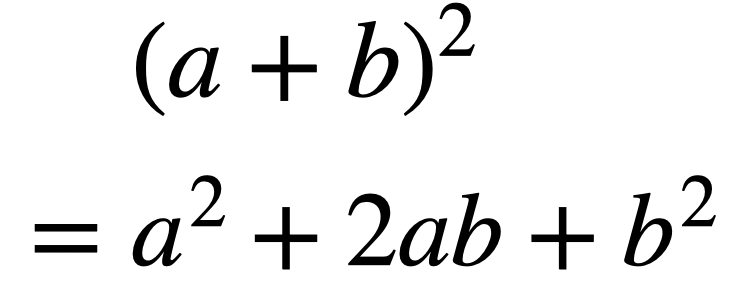
では覚え方。式の3カ所に丸とか印をつけます。
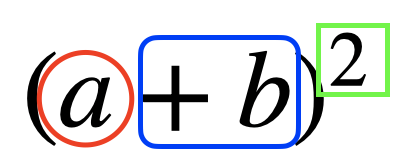
この公式で\(a^2\)と\(b^2\)は気付きますよね。
よくあるのが真ん中の\(2ab\)が消えて無くなるケースです。
それがなくならないように、真ん中は

と覚えてください。
ほら、\(2ab\)になったでしょ笑
だからこの公式は「前2乗、全部掛け、後ろ2乗」と覚えましょう。
はっきり言うとインチキ技です笑。だってカッコの外にある2は2乗を表すで2倍を表すものではないからです。
でも、これでテストはできちゃんですよ。だったらいいじゃないですか。
いろんな教え方してきましたが、この教え方が一番生徒ができるようになります。
では、練習。
\((x+3y)^2\)「前2乗、全部掛け、後ろ2乗」ですよ!
今回は\(x\)と\(+3y\)と\(2\)だから、
\(x^2+6xy+9y^2\)になります。なりましたか?
教科書の例題をいくつかといてコツをつかんで下さいね。間違いなく解く速さがアップするしミスも減りますから。
\((a-b)^2=a^2-2ab+b^2\)の使い方
これは今紹介したのと同じです。
ただ、和ではなく差になるので、真ん中の符号が\(-\)になります。
真ん中の符号に注意してくださいね。
\((x-3)^2\)「前2乗、全部掛け、後ろ2乗」
\(x^2-6x+9\)\((a+b)(a-b)=a^2-b^2\)
これは「和と差の積」のパターンと言われるものです。
カッコの左も右も\(a\)と\(b\)なのは同じですね。
違うのは真ん中の\(+\)と\(-\)の符号だけです。
このパターンの覚え方は
「和と差の積は2乗引く2乗!」です。
()内の左の項を2乗して、”-“を書いて右の項を2乗する。
それだけです。
\((x+3y)(x-3y)\) \(=x^2-9y^2\)慣れたら簡単と思えるから頑張って。
いよいよ因数分解のコツです。
では今までおさらいした乗法公式を使って因数分解を簡単にやるコツです。
まずは、\((x+a)(x+b)=x^2+(a+b)x+ab\)のパターンです。
この公式の呪文は「足して、かける!」でしたね。
今度はその逆をやっていけばいいわけです。
例えば、\(x^2+5x+6\)の場合、1番右の項である6から考えます。
なぜなら掛けてできた数字の組合せの方が、足して出来る数字の組み合わせよりもパターンが少ないからです。
掛けて6は\(1 \times 6\)と\(2 \times 3\)だけです。(あとは符号の組み合わせだけですね)
足して\(+5\)になる組み合わせは負の数考えると無限大に増えますから笑
ですから、まず数字だけの部分に注目して掛けて+6になる組み合わせを考えます。
そして+6になる組合せのうち、足して+5になるものを見つけます。
この場合は、考えられるのは4つの組合せ。
\(+1\)と\(+6\)、\(+2\)と\(+3\)
\(-1\)と\(-6\)、\(-2\)と\(-3\)
ただ、符号に注目すると「掛けて+で足して+」になる2数は+と+しかないので、上の2つに絞られます。
だから問題を解くときに、まず符号を注目するんですね。
超重要:符号の見抜き方
符号の見抜き方には4つパターンがあります。慣れたらすぐに使えるようになります
要は、
- 「掛けて+足して+」
- 「掛けて+足してー」
- 「掛けてー足して+」
- 「掛けてー足してー」
- 掛けて+のパターンは2数が「++」「ーー」の同符号の組み合わせになります。
このときに\(x[/larex]の係数を見て「+」なら「++」、「ー」なら「ーー」になります。
- 掛けてーのパターンは2数が「+ー」の異符号の組み合わせになります。
このときに\(\)x[/larex]の係数を見て「+」なら「数字が大きい方が+」、「ー」なら「数字が大きい方がー」になります。
時短する方法
テストは時間があるから因数分解のスピードも速い方がいいですね。速ければ宿題も早く終わるから早くゲームが出来たり、動画を見ることが出来ますよね。では、どうすればいいのか?
私は因数分解を解くときにははじめに 、\(\)(x- )(x- )\)と先にーの符号まで書いちゃいます。
だって、+だったらチョンって付ければいいからです。
もし+を先に書いてしまうと、消しゴム使わなければなりませんよね。だから先にーを書いておくんですよ。
くだらないなあと思って人。正解です笑。だけど、これ意外方法に慣れるとちゃっちゃかと消しゴムを使わずに因数分解が解けるようになるのでオススメです。
\((a+b)^2=a^2+2ab+b^2\),\((a-b)^2=a^2-2ab+b^2\)のパターン
このパターンを見抜くには、ある数字に注目します。
ある数字とは、「平方数」です。
「平方数」とは同じ数を2回掛けた数字です。
1,4,9,16,25,36,49,64,81,100,121,144,169,196,225…
のことですね。これを因数分解を解く時はこの平方数を頭の片隅にいつも意識するようにしておきましょう。解くのが圧倒的に早くなりますから。
例えば、\(x^2+14x+49\)
まず、1番左の数字だけの項に注目します。その数が「平方数」なら\((a+b)^2,(a-b)^2\)のパターンになる可能性が高いです。
この場合、49なので平方数ですね。ですから\((a+b)^2,(a-b)^2\)のパターンになる可能性が大です。これがどの数の2乗の数かを頭にキープしておきます。
次に注目は\(x[/lataex]についてる数字です。これがさっき頭にキープした数の2倍になっていたらビンゴ!です。
あとは真ん中の符号に注意して完成させましょう。
この問題だと49は\(\)7^2\)ですね。7の2倍は14です。ビンゴ!ですね。
だからあとは真ん中の符号が+なので\((x+7)^2\)になります。
だから「平方数」を意識しましょう。
\((a+b)(a-b)=a^2-b^2\)
最後に和と差の積のパターンです。
これも慣れると「ラッキー!」と思えるようになります。
見極め方は、ズバリ「項の数」です。
因数分解で乗法公式を使う場合、1から3までのパターンは項が3つです。
でもこの「和と差の積のパターン」だけは項が「2つ」なのです。
しかも、符号が「ー」です。
そして和と差の積のパターンの呪文は「2乗引く2乗」でしたね。
と言うことはここでも「平方数」が活躍してくれるのです。
例えば、\(36x^2-25y^2\)
これは\((6x)^2-(5y)^2\)になるので、
\((6x+5y)(6x-5y)\)が正解です。
なので、平方数は大切なのです。ですから上で紹介した1から15の平方数「1から225」までは覚えておくといいですよ!
最後に1問
これが出来たらOKです。
\(4x^2-36y^3\)さあちょっと考えてみて解いてください。
正解出ましたか?
……
正解は\((2x+6y)(2x-6y)\)ではありません!
えっ!?と思ったあなた。でも違うんです!
なぜか、それは因数分解の大鉄則を使ってないからなんです。
因数分解の大鉄則を覚えていますか?
それは「共通因数でくくる」でしたね。
この問題の場合4が共通因数なので、まず4でくくらなければなりません。
ですから、正解は
\(4(x+3y)(x-3y)\)になるのです。
出来た人はすごいですよ!
この問題はひっかけ問題として良く出題されます。
まとめ
どうでしたか?
なるほど、すごい、当たり前じゃん、よく分からん、いろいろ意見はあると思います。
はっきり言って勉強なんて慣れだから、繰り返し頑張ってみてよ。
因数分解出来ないから負い目に思う必要なんてない。だけど出来た方がバカにされないし、楽しいじゃん。割とゲーマーの生徒は因数分解はパズルみたいだから面白いと言うことが多い気がする。だから「勉強」なんて身構えないで、ゲームみたいに工夫して楽しめればといいと思う。
このサイトでは勉強で悩んでる人向けに解き方を伝えていこうと思う。取り上げて欲しい問題があったらコメントなりお問い合わせフォームから連絡くださいね。もちろん全てには答えられないけど笑