[mathjax]今回は、たすき掛けの因数分解が苦手な人、時間がかかるのでもっと速く解きたい人に向けた内容です。
- 普通の因数分解ならなんとか解けるけど、たすき掛けは数字の組み合わせがいっぱいあって何回も試さなきゃいけないから大変だし正直面倒くさい…
- でもできるにならないテストで赤点取っちゃったらかっこ悪いし、
- 赤点取ったら再試があるし、休みに補習出なくちゃいけなくなるのはもっとやだ!
- お姉ちゃんからたすき掛けできないとこの先の二次方程式とか数学人生詰むぞ!って脅かされてる。
- 明日のミニテストのためにたすき掛けのスピードをアップさせたい!
どれか一つでも思い当たったら読んでみてくださいね。
では、いってみましょう♫
たすき掛けの因数分解とは
たすき掛けの因数分解とは、因数分解を解く手法の1つです。中高一貫校であれば中学校で扱う場合がありますが、本来は高校1年で学ぶ「数Ⅰ」で学ぶ手法です。
\(x^2\)の係数(前についてる数字)が2以上の場合に使うことが多いです。

こんなの見たことありませんか?
青い線と赤い線のところがたすきにかけてありますよね。
だからたすき掛けって言います。
具体的な数字だとこんな感じ。
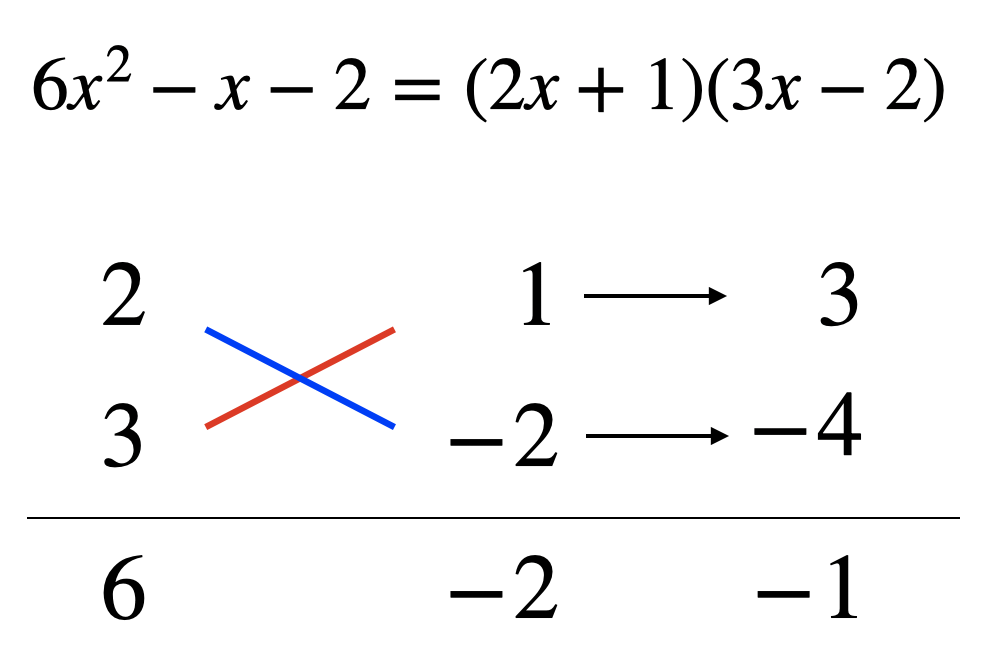
なぜ、たすき掛けの因数分解は面倒くさいのか?
たすき掛けの因数分解が面倒くさいのは「数字の組み合わせ」がたくさんあるからです。1回や2回でドンピシャ決まると気持ちいいですが、そうでないとイライラしますよね。
例えば上の問題の場合符号との組み合わせを考えると8通り考えられます。
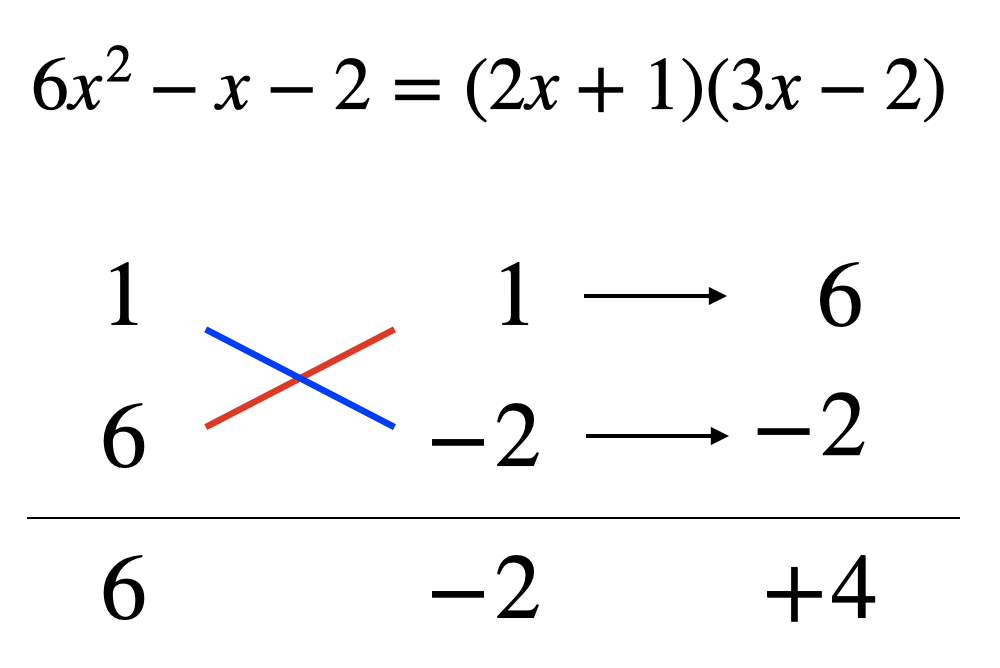
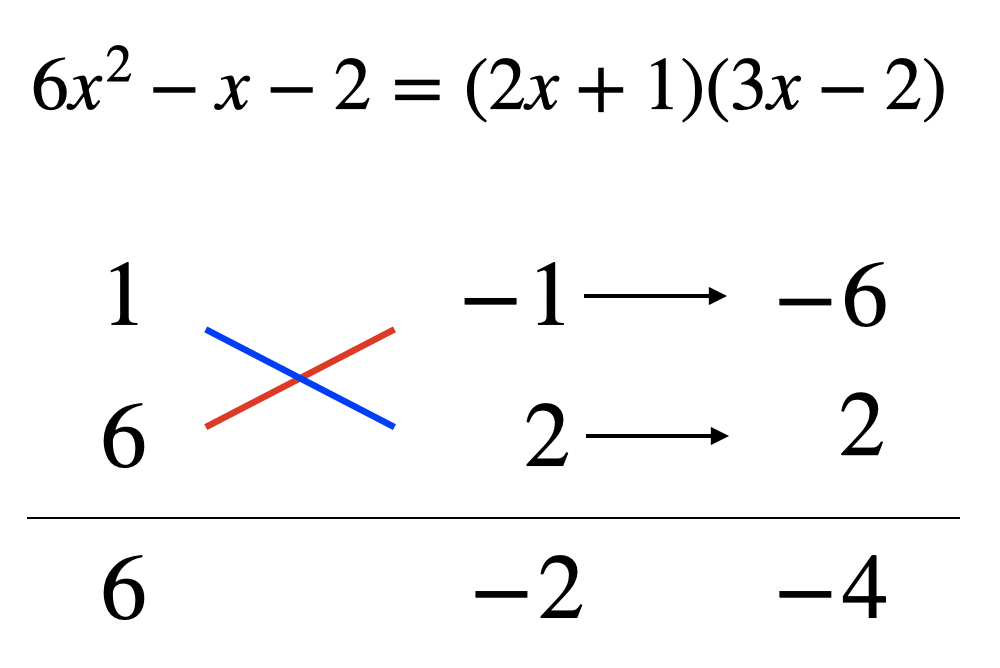
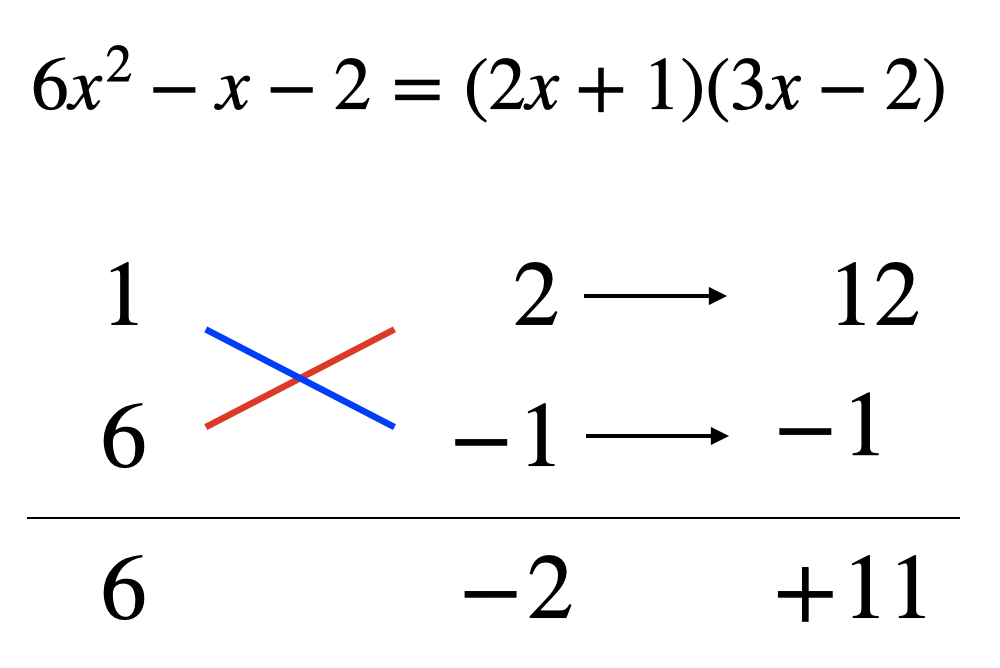
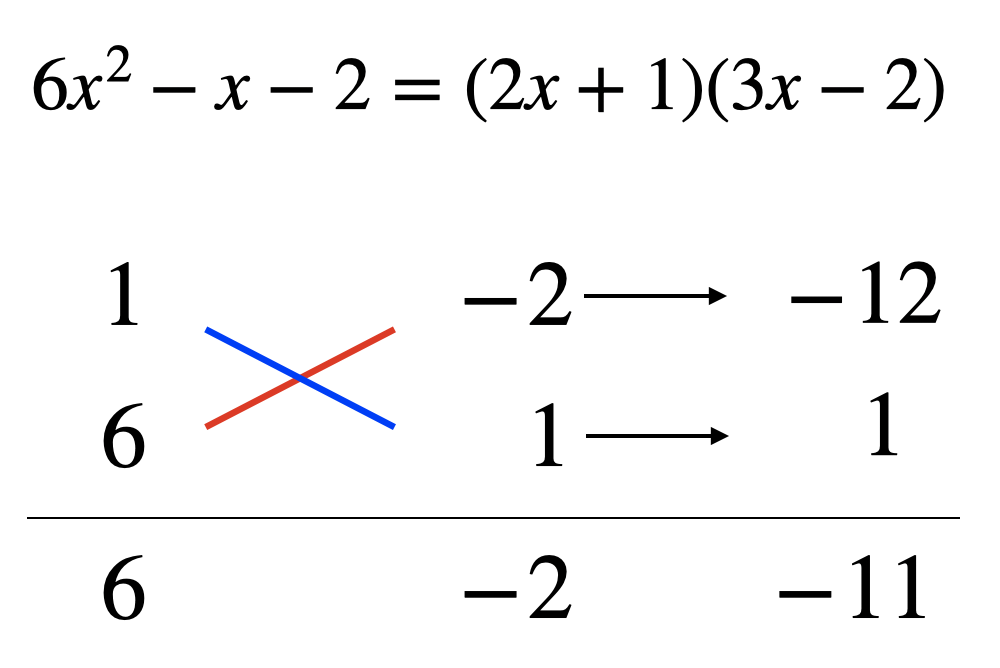
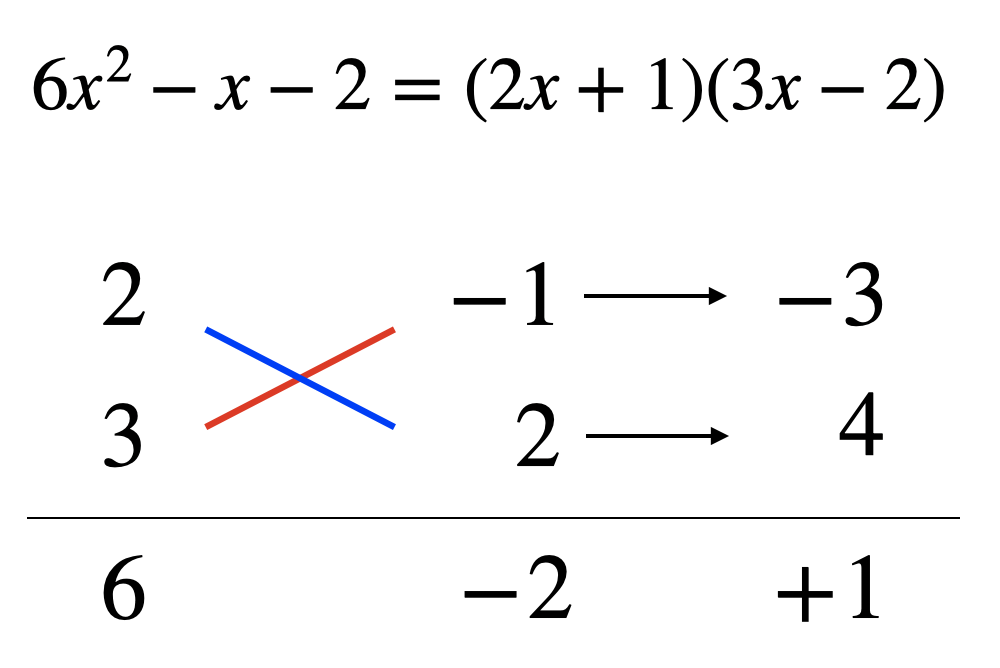
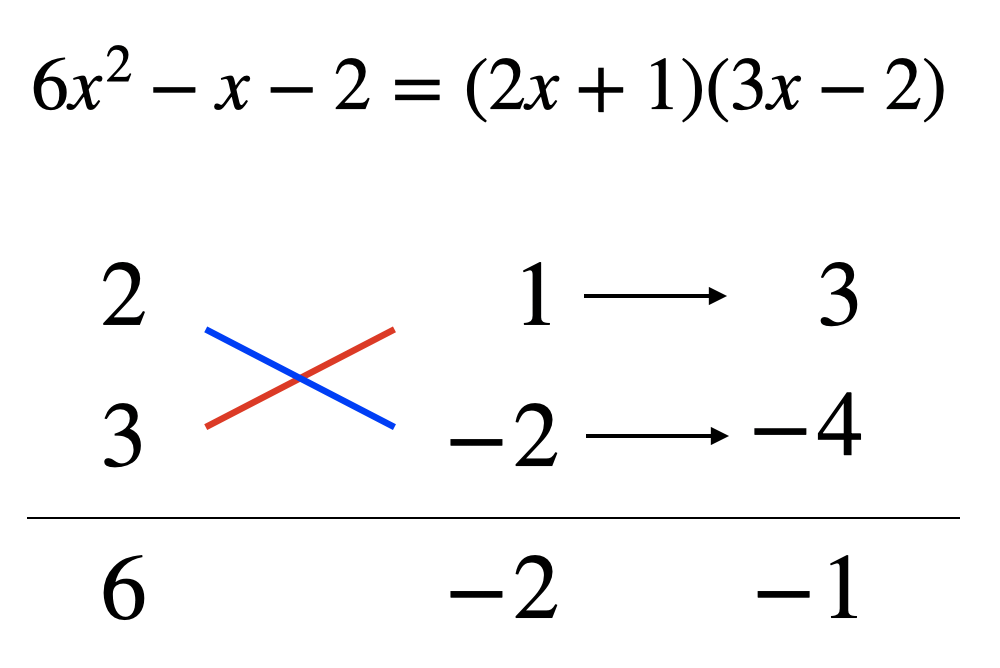
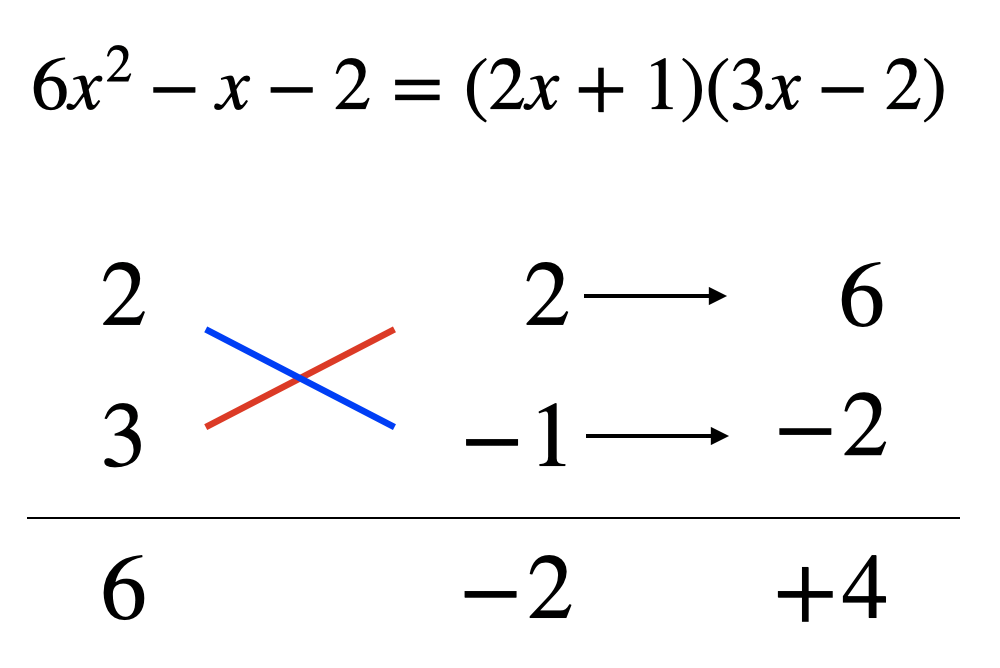
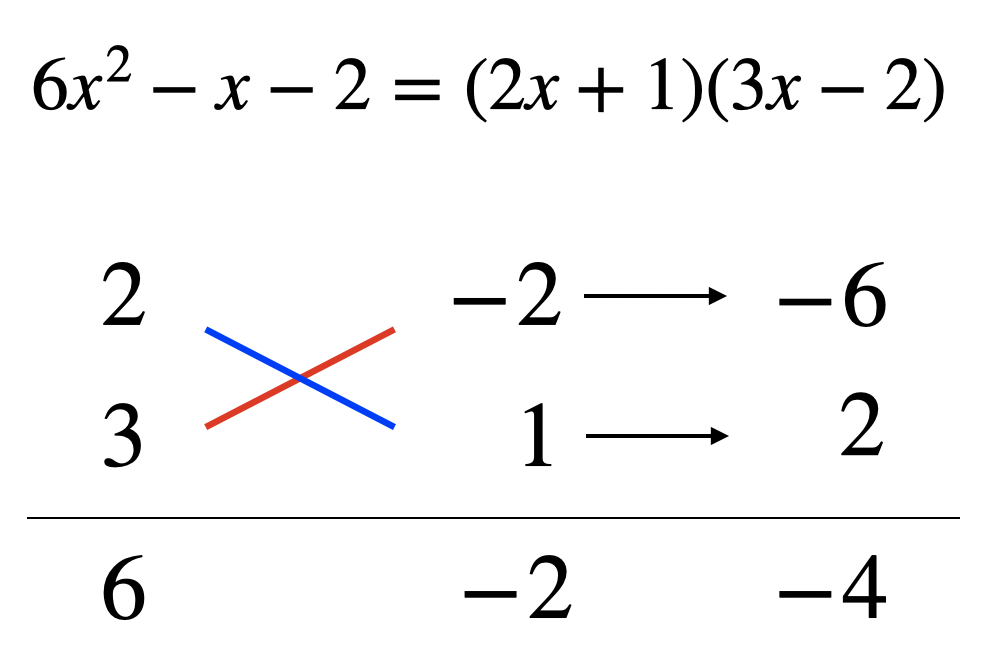
この問題は定数項が2なのでまだ組み合わせは少ない方なんですよね……。
数字の感覚があるとスラスラできるのですが、数学に苦手意識があったりすると思うように解けなくて挫折するわけです。
でも、この組み合わせの数を減らすことができれば、楽チンだと思いませんか?
そんな技も含めて「たすき掛けを簡単に解く3つのコツ」を紹介します!
たすき掛けの因数分解を簡単に解く3つのコツ!
では、たすき掛けの因数分解を簡単に解く3つを紹介します。
- 互いに素を意識する
- 符号の組み合わせを意識する
- 2つ目の文字は解答用紙に先に書いておく
です。
ではそれぞれ詳しく説明しますね。
1.互いに素を意識する
いきなり「互いに素」なんて難しい数学用語出すんじゃないよって思ったかもしれませんが、実はそんなに難しくなくて(むしろ簡単)約数が1だけってことです。
具体例で見ていきます。
今回は因数分解なので2つの数とします。
例えば、6と5。この2数は1でしか割れませんよね?こういうのを「互いに素」って言うんです。
6と2では、2で割り切れるので互いに素ではありません。
因数分解の大鉄則は「共通因数でくくる」でしたね。
だから括弧()の中の数の約数は1意外あり得ないのです。なぜならそれ以外の約数がある場合はすでに共通因数として()の外にくくり出されているからです。
ですから次の下段にある6と+2や2と−2の組み合わせは、答えとしてあり得ないんですね。
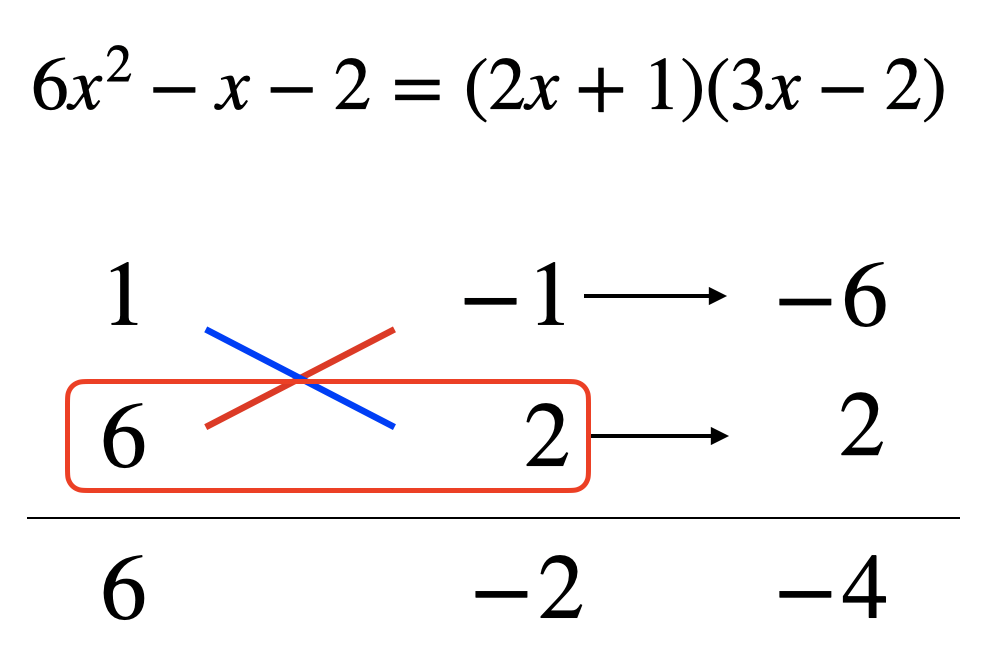
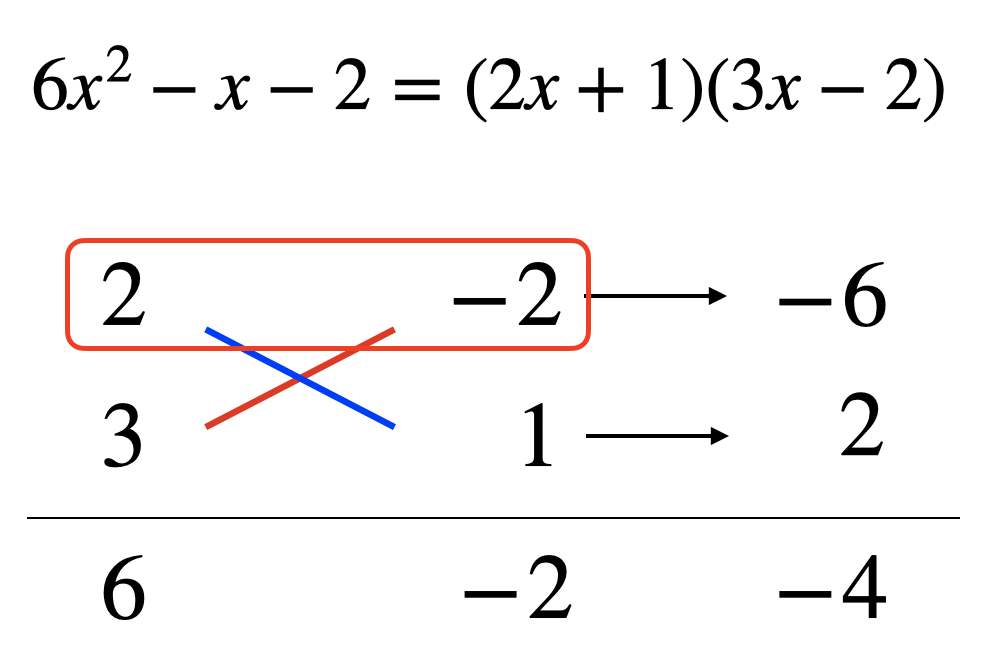
だからはじめから考えなくていいんですよ。そうすると考えるパターンが8種類から4種類にまで半分で済むんですね。少し楽になって来ましたね。
2.符号の組み合わせを意識する
2つ目のコツは「符号の組み合わせを意識する」です。
例えば上の問題\(6x^2-x-2\)、1番右の定数項(数字だけの項)の符号が「ー」です。
ということはかける2数のうち1つの符号は「ー」が確定します。しかも真ん中の項の符号は「ー」です。
そうするとたすき掛けしてできた2つの数字のうち絶対値(数字)が大きい方が「ー」になるわけです。なぜなら足してマイナスの数になるには絶対値が大きい方がマイナスの数出なければマイナスの数にならないからです。
この問題は「符号の組み合わせ」だけを考えた場合にも8種類から4種類に減ります。
しかも「互いに素」も組み合わせれば、この問題の場合組み合わせは次の2通りだけになります。
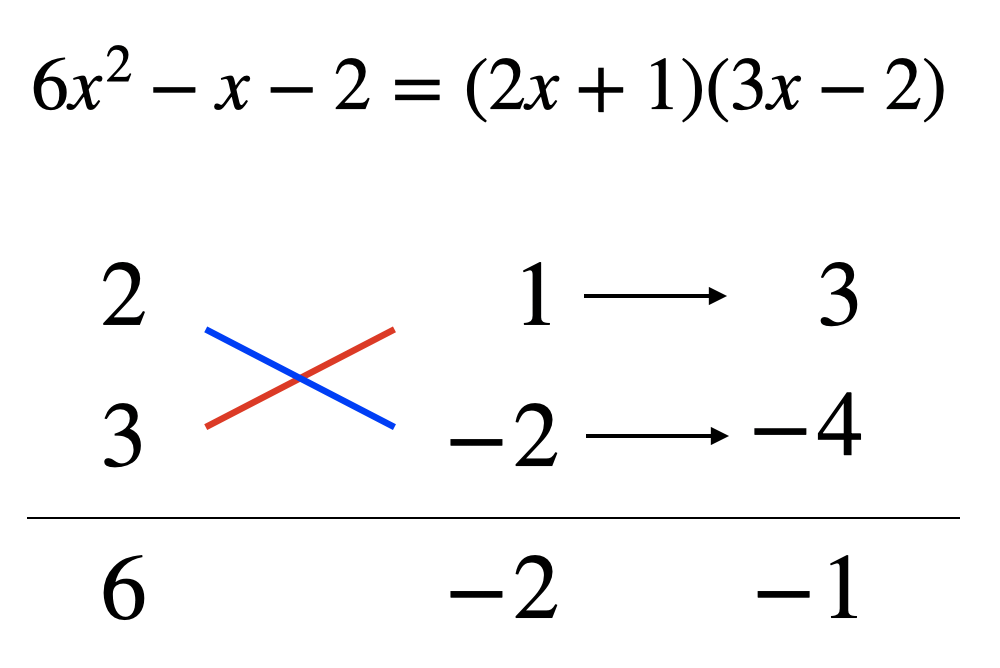
こっちが正解
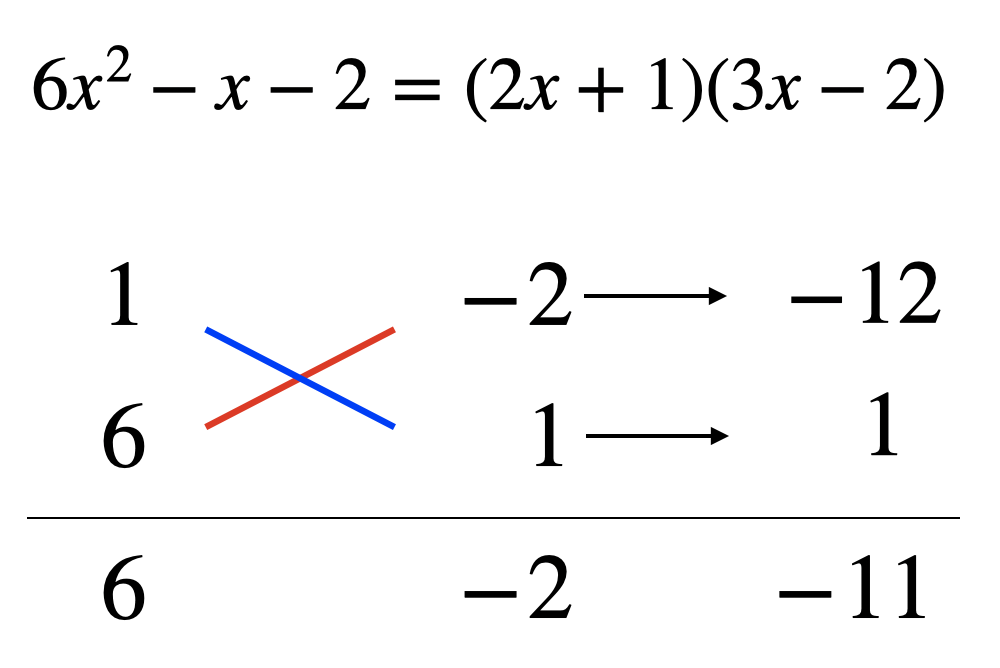
こっちは不正解
8種類あるのが「互いに素」と「符号に意識」するだけで2種類だけ考えればOKなんですよ。
これならかなり楽ちんになりますよね!
2つ目の文字は解答用紙に先に書いておく
たすき掛けの因数分解を簡単に解く3つのコツの最後はミスを減らすチート技です。
上の問題のように\(6x^2-x-2\)文字が\(x\)だけと1種類だと問題なのですが、これが\(6x^2-xy-2y^2\)のように 文字が2種類出てくるときにやってしまいがちなミスを減らす技です。
たすき掛けって数字だけを取り出して考えるので、例えば\(6x^2-xy-2y^2\)の場合、解答欄についうっかり\(=(2x+1)(3x-2)\)と書いてしまうんですよ。\(y\)を書き忘れちゃうんです。
本来なら\(=(2x+y)(3x-2y)\)と書かなければなりません。
でもついやっちゃうんですよね、解けた!って気持ちがほっと気が抜けるんでしょうね。
あなたもやったことありませんか?(私は学生時代に何回もやったことがあります)
このミスを減らすには、次のように解答欄に先に文字を書いておくんですよ。
( \(\ x\) –\(\ \ y\))( \(\ x\) –\(\ \ y\))
文字の前に少しスペースを開けておくのがコツです。符号の「ー」は先に書いておきましょう。「+」だったらチョンと書き足せばいいだけですから。
これだけでミスは減るしスピードもアップするし、軽快に溶けるようになりますよ。
まとめ
たすき掛けの因数分解を簡単に解く3つのコツ!をまとめると、
- 互いに素を意識する
- 符号の組み合わせを意識する
- 2つ目の文字は解答用紙に先に書いておく
です。
勉強なんて慣れですから、繰り返しやっていればそれなりには解けるようになりますから。
ぜひコツを試して、たすきがけの因数分解を少しでも早くミス無く解けるようになってくださいね。
