「先生!点が動くって意味がわかんないんだけど!」
昨日の授業でとキレ気味で質問されました笑
一次関数は苦手意識を持つ生徒が多い分野です。ただでさえ苦手なのに、さらに点が動くとか意味が分からないし、どうやって解けばいいのか?
その「動点問題」の解き方を基本から分かりやすく解説していきます。
中2数学の一次関数の問題である意味ラスボス的な存在である「動点問題」。そんなラスボス対決のための手順を2つのパターンに分けて説明します。
一次関数の動点問題で出題される2つのパターン
下の問題を見てください。図は同じです。ただし違うところがあります。どこが違うでしょうか?
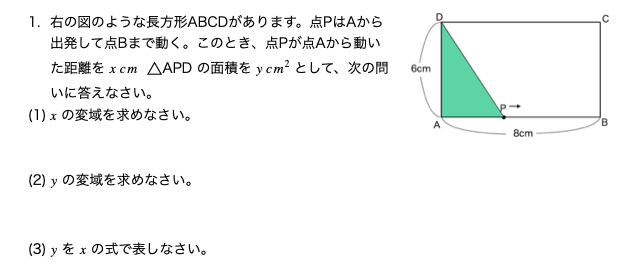
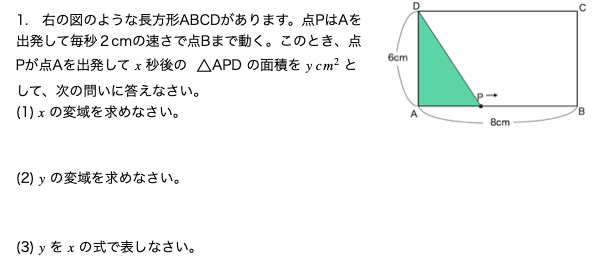
違う点がわかりましたか?
そうです。上の問題は \(x \)が長さだったのに対して、下の問題の \(x \)は時間(秒)になっています。
当然この違いは解き方の違いになるので、まずはここをしっかり確認しましょう。
一次関数の動点問題:\(x \)が長さの場合の解き方
まずは、\(x \)が長さの場合の解き方の説明から。
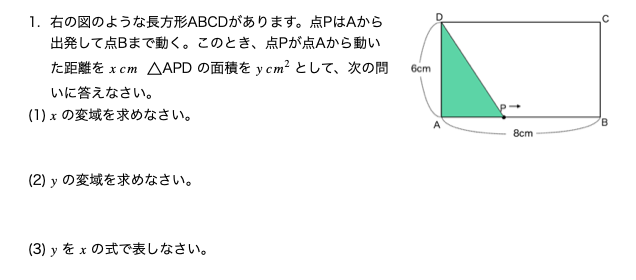
関数の利用の問題を解くときに重要なのは、\(x \)と\(y \)がそれぞれ何を表しているのかを把握することです。これがきちんとわかってないと問題は解けません。この問題の場合は\(x \)が長さで\(y \)は\(\triangle \textrm{APD}\)の面積です。
なので、三角形の面積の公式を思い出しましょう。
三角形の面積=底辺×高さ÷2 でしたね。
ということは、底辺と高さが分かればこの問題は解けることになります。
ここでは辺ADを高さ、辺APを底辺として\(\triangle \textrm{APD}\)の面積を考えてみましょう。
AD=6、AP=\(x \)になりますね。これを頭に入れて実際に問題を解いていきましょう。
では(1)から解説します。
(1) \(x \)の変域を求めなさい。
(1)は\(x \)の変域の問題です。
\(x \)の変域とは、\(x \)の変わる範囲のことです。一番短いときの値と一番長いときの値を考えて不等号で表します。
\(x \)は点Pが点Aから動いた距離を表します。ですから一番短いのは「点Pがまだ動いていないとき」=「点Pが点Aと重なっているとき」ですね。ですから 0 cm になります。
点Pは点Bまで動くので、一番長いときは点Pが点Bにいるときなので、8 cm になります。
よって、答えは 0 \(\leqq \) \(x \) \(\leqq \) 8 になります。
*中には面積が0なら三角形にならないので、0は含まないので、
(2) \(y \)の変域を求めなさい。
(2)は \(y \)の変域の問題ですね。
\(y \)は\(\triangle \textrm{APD}\)の面積でしたね。なので、\(\triangle \textrm{APD}\)の面積が一番小さいときの値と、一番大きいときの値を求めて不等号で表せばいいわけです。
AD=6、AB=\(x \)で、変化するのは\(x \)なので\(x \)の値によって面積が変化します。
\(\triangle \textrm{APD}\)の面積が一番小さいときって点Pがどこにあるときでしょうか?
それは点Pが点Aにあるときです。そのときの\(x \)の値は(1)より0でした。底辺が0なので面積は0になります。
次に面積が一番大きい時って点Pがどこにあるときでしょうか?
点Bにあるときが底辺が一番長くなるので面積が最大になります。
そのときの\(x \)の値は辺ABの長さと同じになるのでAB=8になります。
よって、三角形の面積を求める公式に値を代入して計算すると、
\(\triangle \textrm{APD}\)=8×6÷2=24
になります。最小値が0で、最大値が24になるので、答えは
0 \(\leqq \) \(y \) \(\leqq \) 24
*先生の中には面積が0のときは三角形にならないので0を含まないと指導される方もいます。
その場合の答えは、0 <\(y \) \(\leqq \) 24 になります。担当する先生の指導に合わせてください。
(3) \(y\)を\(x\)の式で表しなさい。
「\(y\)を\(x\)の式で表しなさい」とは「\(y=\)」の形の式で表すことです。
この問題で\(y\)は\(\triangle \textrm{APD}\)のことでしたね。ですから三角形の面積の公式の通り\(x\)を使って面積を表せばいいわけです。
三角形の面積=底辺×高さ÷2
\(\triangle \textrm{APD}\)=\(x\)×6÷2 を計算して
\(y=3x\)
これが答えです。
一次関数の動点問題:\(x \)が時間の場合の解き方
今度は\(x \)が時間の場合の解き方です。
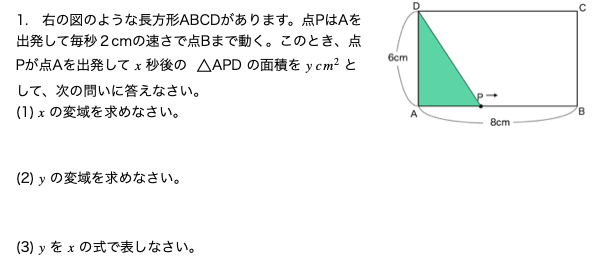
コツ:時間\(x \)と速さ(毎秒2cm)から底辺を\(x \)を使って表す。
この問題の場合は\(x \)が時間なので、ここからAPの長さを計算する必要が出てきます。なのでこっちの問題の方が若干レベルが上なわけです。
では時間から長さを求めるにはどうすれば良いのか?
ヒントは点Pの速さが毎秒2cmです。
速さと時間が分かれば距離は計算できましたね。
距離=速さ×時間
でした。ですからAPの長さは2×\(x \)になるので、\(2x \)と表せます。
この考えが難しいと思う人は次にように考えてもいいですよ。
毎秒2cmとは、1秒間に2cm動くということです。2秒なら4cm、3秒なら6cm、4秒なら8cmですね。
1秒 → 2cm
2秒 → 4cm
3秒 → 6cm
4秒 → 8cm
問題文には\(x \)秒後の\(\triangle \textrm{APD}\)を\(y \)とする。と書いてあるので\(x \)を使ってAPの長さを表します。
上の流れから時間の2倍が長さだとわかります。よってAPの長さは2×\(x \)になります。
では、問題を一緒に解いていきましょう。
(1) \(x \)の変域を求めなさい。
今回の問題の場合、\(x \)は時間でした。そして点Pは点Aから点Bまで動きます。
何秒かかるでしょうか?
毎秒2cmで動くので8cm動くのには4秒かかりますよね?よって最大の値は4ということです。
よって、
0 \(\leqq \) \(y \) \(\leqq \) 4
が答えです。
(2) \(y \)の変域を求めなさい。
この問題の考え方は上の(2)の問題と同じです。\(\triangle \textrm{APD}\)の面積の最小値と最大値を求めればいいので、
0 \(\leqq \) \(y \) \(\leqq \) 24
が答えです。
(3) \(y\)を\(x\)の式で表しなさい。
\(y\)は\(\triangle \textrm{APD}\)のことなので、三角形の面積の公式の通り\(x\)を使って面積を表せばいいわけです。
\(x\)は時間、秒速は2cmという条件を使って底辺を表します。上のコツで説明した通りAP=2\(x \)と表せるので、公式に当てはめて
公式:三角形の面積=底辺×高さ÷2
\(\triangle \textrm{APD}\)=\(2x\)×6÷2 を計算して
\(y=6x\)
が答えです。
テストによく出題される例

はじめの2問は点Pが点Aから点Bまでしか動きませんでした。この問題はさらに点Cを通り点Dまで動きます。
このように角で曲がる問題は、点PがA→B、B→C、C→Dのそれぞれの区間で三角形の変化の仕方が変わるので場合分けして考えていきます。今どの区間にあるのかを把握してその区間だけに集中して問題を考えましょう。
(1)点PがAからBまで動くときについて下記の問いに答えなさい。
ここは1つ上の問題と同じなので省略します。
(2)点PがBからCまで動くときについて下記の問いに答えなさい。
(ア) \(x \)の変域を求めなさい。
(ア)は\(x\)の変域の問題です。変域の問題は最小値と最大値を求めれば良かったですね。
最小値はもちろんBにいるときですから、\(x\)は4になりますね(8÷2=4)。(\(x\)は時間ですから距離÷速さで求めます)
最大値はCにいるときですから、6÷2=3でさらに3秒かかるので4+3=7になりますね。もちろんAからBを通ってCまでの長さ14(8+6)を求めてから14÷2=7と計算してもOKです。よって、
4 \(\leqq \) \(y \) \(\leqq \) 7
が答えです。
(イ)\(y\)を\(x\)の式で表しなさい。
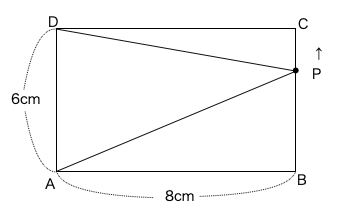
点PがBからCに移動しているとき、Pから辺ADにおろした垂線はずっと8cmになります。
よってこの区間はADを底辺、Pからおろした垂線を高さと見ると、底辺は6cm、高さは8cmの固定になるので、
\(\triangle \textrm{APD}\)の面積は、6×8÷2=24になります。
よって答えは、
\(y=24\)
になります。右辺の24に\(x\)はつかないので気をつけましょう。
(3)点PがCからDまで動くときについて下記の問いに答えなさい。
(ア) \(x \)の変域を求めなさい。
点PがCにいるとき、点Aから点Bを通って点Cまで8cm+6cm=14cm移動しています。
かかる時間は、14÷2=7秒
点Dまでさらに8cmなので、8÷2=4。よって、7+4=11秒かかります。
したがって、\(x \)の変域は
7 \(\leqq \) \(y \) \(\leqq \) 11
になります。
(イ)\(y\)を\(x\)の式で表しなさい。
さあラスボスです。これが出来たら動点問題に自信を持っていいいですよ。
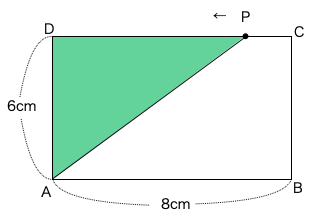
\(\triangle \textrm{APD}\)の底辺をAD、高さをPDと見ます。AD=6なので、あとはPDの長さを\(x\)を使って表すことができれば、公式に代入して式を立てることができます。
ではPDを\(x\)を使って表すとどうなりますか?よくあるのが8-\(2x\)です。CDの長さが8cmなので一見合っているように思えますが、違います。
なぜかというと、8-\(x\)という式では\(x\)はCPの長さを表します。ところが点Pってどこから出発したのでしょうか?
問題文に「点Pが点Aを出発して」と書いてあります。そうなるとAB+BC+CP=\(x\)ということになります。
なので、点Aから考えなくてはなりません。下の図がそのイメージです。
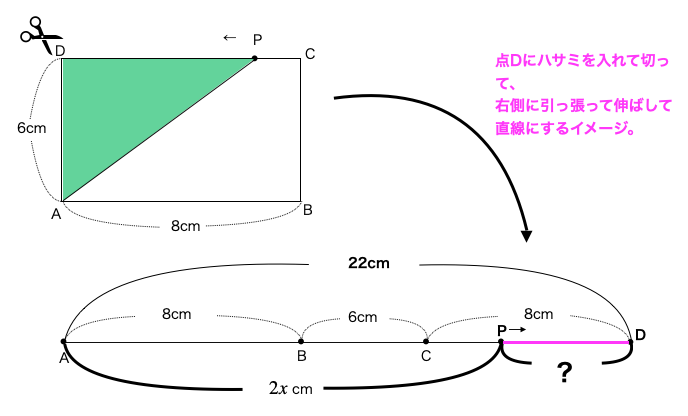
イメージできましたか?
上の図を見れば、PDの長さはAD-APで求められることが理解できると思います。
よって、PD=AD-AP=22-2\(x\) になります。
あとはこれを使って\(\triangle \textrm{APD}\)の面積の面積を表しましょう。
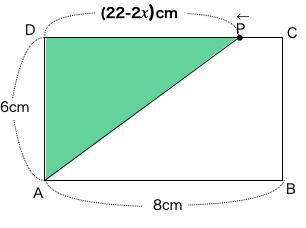
\(\triangle \textrm{APD}\)の面積=底辺×高さ÷2=AD×PD÷2=6×(22-2\(x\))÷2
これを計算して、\(\triangle \textrm{APD}\)=-6\(x\)+66 になるので答えは
\(y\)=-6\(x\)+66
になります。
別解:\(y\)を\(x\)の式で表す問題をもっと簡単に解く方法
今までは図形的な発想でこの問題を解いてきました。でも中には図形が苦手な人もいるはず。
そこで、もっと計算でスラスラと解く方法を説明します。
それは対応表を作って計算して解く方法です。これなら一次関数の2点から直線の式を求める方法で解けます。
点PがA、B、C、Dにあるときの\(x\)と\(y\)を計算して下のような対応表を作ります。この問題の場合\(x\)は距離(\(cm\))ではなく、時間(秒)なので気をつけてくださいね。(*時間=距離÷速さで求めましょう。例えば、点Aの\(x\)を求める場合、AB間の距離=8cm、速さは秒速 2cmなので、8÷2=4になります)
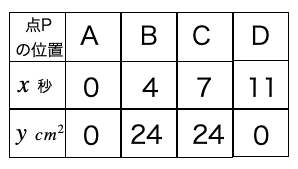
この表を参考に、連立方程式や一次関数の変化の割合の求め方から式を求めていけばいいのです。
上の表を座標に置き換えれば、A( 0 , 0 )、B( 4 , 24 )、C( 7 , 24 )、D( 11 , 0 )になるので、座標の方が計算しやすい人はこのように変換して解いてください。
人それぞれ求めやすさの違いがあるので、自分が求めやすいやり方で練習してください。
まとめ:一次関数の動点問題の解き方
・\(x\)や\(y\)が何を表しているのかを把握する。
・点Pがどの区間にいるのかをしっかり場合分けをして、その区間に集中して考える。
・図形で考えるのが難しいときは対応表を使って代数的に考える。
どうでしたか?解き方を理解したら、実際に手を動かして練習しましょう。問題を繰り返し解くことで、一次関数の中でラスボス的な存在である動点問題を楽々と解くことができるようになるでしょう。
分かった(理解できた)と出来るは同じではありません。まずは「理解する」こと、そして問題を解くことを繰り返して「出来る」ようになりましょう。
