こんにちは!
今日は一次関数が苦手な人が得意になるための考え方や問題の解き方をレクチャーします。
この記事を読めば、一次関数のざっくりとした意味合いが分かり表やグラフから直線の式を求められるようになります。
この記事を読んだ方がいい人
- 一次関数の基本がわからない人
- 一次関数の表から直線の式を求められない人
- 一次関数のグラフから直線の式を求められない人
- 一次関数を得意にしたい人
では、いってみよう!
一次関数が苦手な人にまず意識して欲しいこと
苦手に人は一次関数の基本的な意味合いがわかっていない場合がほとんどです。
基本的な意味を理解して手順を踏んで問題を解いていけばできるようになります。
ですから、まずは一次関数とはどんな意味なのかざっくりとでいいので理解しましょう。このときのコツは意味を視覚的にイメージして理解することです。
その次に\[y=ax+b\] という式は何を表しているのかを理解しましょう。
その上で問題を解いて練習していけば必ず解けるようになります。
ざっくりと意味を理解してイメージしよう
意味を理解するときに大切なことは、その状況を視覚的なイメージをしながら理解していくことです。
もちろん中には文章(テキスト)で理解が進む人もいます。ただ、長年の経験やその手の本を読むと視覚的に理解することが優位な人が多いという印象です。
私も新しいことを理解するときはできるだけ写真のようにイメージするようにしています。そうすると理解も進むし比較的楽に覚えられます。私は写真のように静止画で覚えるのが得意ですが、中には動画のように動きを加えて覚えるのが得意な生徒もいます。
どちらが得意なのかは過去の出来事を思い返してみてください。その時に静止画と動画のどちらの方が多いのかで決めてください。
では、実際にイメージをしながら一次関数をざっくりと理解していく練習をしてみましょう。
教科書や参考書を見ると、最初に水槽やバネについての具体的な数字を使って説明があります。中学1年生の時に習った比例と比較して説明する場合が多いです。
そして、
「一次関数は「 \(y = ax + b\) 」のように「\(y\) = 一次式」で表せる関数と定義されています。グラフでは直線で表されます」
みたいに書いてあります。
その通りなのですが、この部分をあまり理解しないで先に進むと苦手意識が深まります。中にはこの段階でなんのこっちゃわからん!となる場合もあります。
なので、まずはざっくりと意味をイメージすることからやってみましょう。
一次関数とは、まず初めにある決まった量があって、そこから一定の割合でその量が増えていく(減っていく)関係のことです。
この初めは\(x=0\)の場合が多いです。今は\(x=0\)の量(値)と覚えておけばOKです。
例えば、初めお風呂に5リットルの水があったとします。
お風呂に水が入っているのを視覚的にイメージしてみてください。頭の中に写真でも動画でもいいので(その人の特性によって得意な方を使ってください)お風呂をイメージしてください。
こんな感じです。

そこから水を1分間に2リットルずつ入れていきますよ。
蛇口から水がドボドボと入っていくところを同じように視覚的にイメージしてください。
どんどんお風呂の水が増えていきますよね。
1分経ちました。水槽の中の水は初めのイメージよりも増えていますね。
では、実際に何リットルになりましたか?
初めに5リットルあって、1分後には2リットル増えているわけなので、5+2=7リットルになりますよね。
2分後はどうなりますか? 3分後はどうでしょうか? 10分後はどうなりますか?
お風呂の中の水がどんどん増えていきますよね。
2分後には9リットル、3分後には11リットル、10分後は25リットルになっています。
今度は水を抜いていきます。
もし1分間に2リットルずつ抜いていくとどうなるでしょうか?
頭の中で水が減っていく様子をイメージしてください。
1分後には、5-2=3リットルになりますよね。
このように初めにある量から一定の割合で増えたり減ったりする2つの関係のことを一次関数といいます。
2つの関係というのは、上のお風呂の例で言うと「時間」と「お風呂の水の量」のことです。
また、一定の割合とは、どんな時も同じスピードで変化が起こることを意味します。
それを式で表すと、\(y=ax+b\) と表されるのです。
上のお風呂の例では、
増える場合:\(y=2x+5\)
減る場合 :\(y=-2x+5\)
と表します。
\(y=ax+b\) の式の\(x\)に付いている(掛けてある) \(a\) は一定に割合でどのように変化をしていく量を表しているので「変化の割合」といいます。(グラフを書くときは「傾き」と言ったりします。後で説明します)
\(b\)は切片と言います。(私が学生の時は\(y\)切片と習った思います)
\(x=0\) の時の \(y\) の値のことです。
今回のお風呂の例では、初め(0分後)に水はすでに5リットル入っていました。だからこの場合 \(b=5\) になります。ここに一定の割合(1分間)に2リットルずつ増やしていきました。だから \(a=2\) になるのです。(減らす場合は \(a=-2\) )
この関係を表で表します。\(x\) を時間、\(y\) をお風呂の水の量を表しています。

この表を見ると、\(x\) が1増えると、y が+2ずつ増えていくことがわかります。
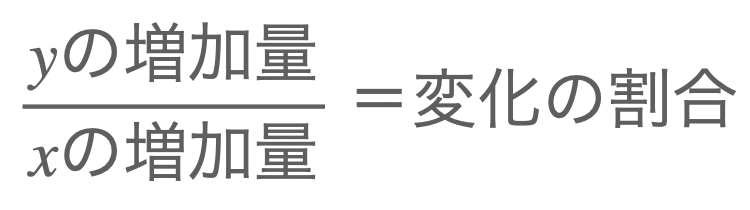
このように \(x\) が1増える(増加量)ときの、\(y\) 増える量(増加量)のことを「変化の割合」と呼びます。
この表から一次関数の式を求めると \(y=2x+5\) となります。
もう一つ見てみましょう。
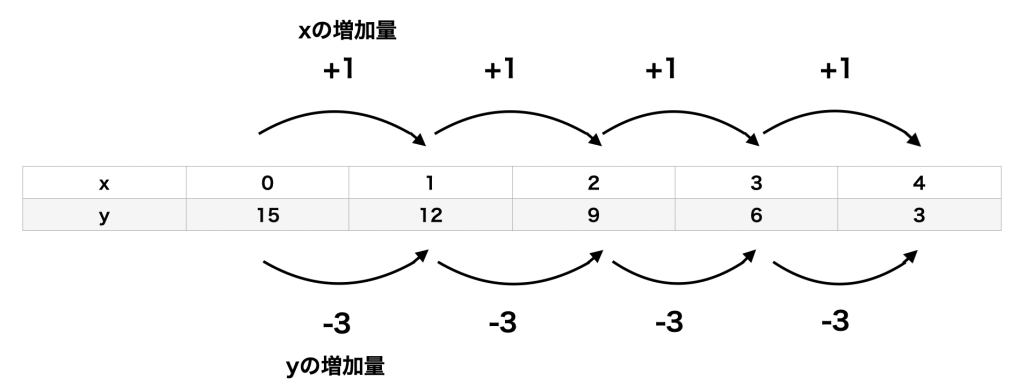
今度の場合は、\(x\) が1増えると、\(y\) が-3ずつ増えていくことがわかります。
(-3ずつ増えることは3ずつ減るのと同じ意味です)
ですから \(a=-3\)であることが読み取れます。
また、\(x=0\)のとき\(y=15\)なので、\(b=15\)が読み取れます。
合わせてこの表の関係を一次関数の式で表すと\(y=-3x+15\)となるわけです。
では実際に問題を解いてみましょう。
表から一次関数の式を求めてみよう
例題:次の表から一次関数の式を求めましょう。
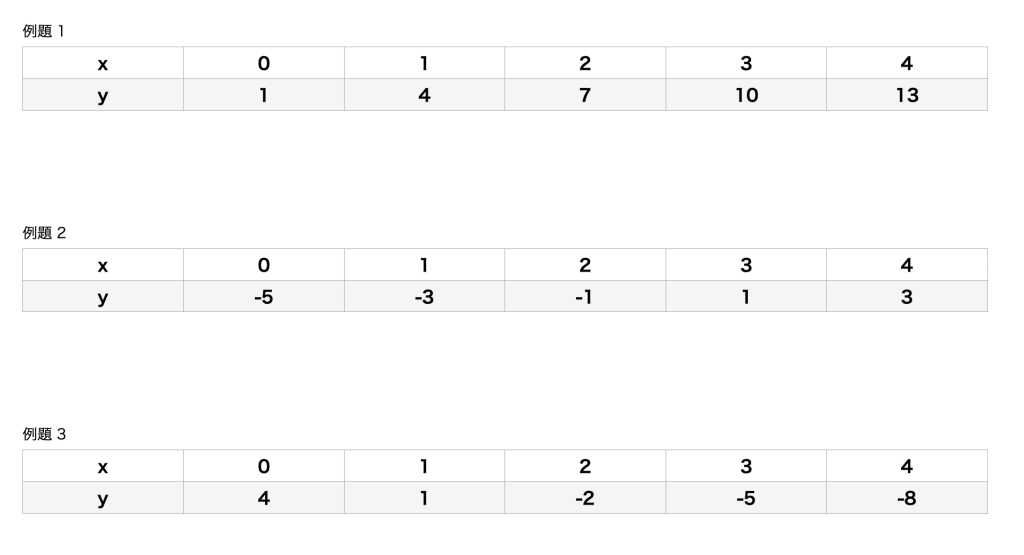
例題の答え
例題1の答え
一次関数の式は\(y=ax+b\)ですから、\(a\) と \(b\) を求めれば良い訳です。
まずは、\(a\) から。
\(a\) は変化の割合でしたね。変化の割合の求め方は
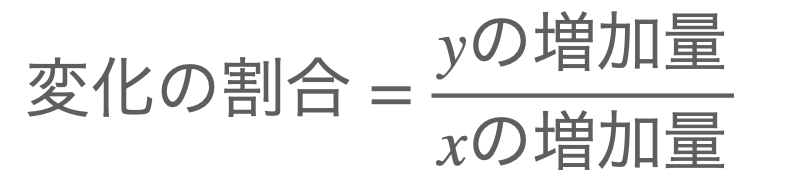
ですね。これで求めた量は、\(x\) が1増えたときの \(y\) の増加量を表します。
例題1の場合、表から3ずつ増えていくのが読み取れます。
ですから、 \(a=3\) になります。
次に、 \(b\) を求めます。
\(b\) は\(x=0\) のときの \(y\) の値のことです。
表から、 \(x=0\) のときの \(y\) の値は 1 であることが読み取れますね。
ですから、 \(b=1\) になります。
よって答えは、
\(y=3x+1\)
です。
・ここで「値」と「増加量」の違いをしっかり押さえましょう。
「値」とは表や座標に書いてある「数字」のことを指します。
それに対して「増加量」とは「差」のことです。引き算して求める量のことです。
一次関数が苦手な人はこの「値」と「増加量」の区別がしっかりできていない場合が多いです。ここの違いをしっかり押さえて練習を積めば一次関数は必ず得意になりますよ。頑張ってください。
例題2の答え
例題1と同じように読み取ってください。
\(y\)の値が \(-5\) から \(-3\) に増えてますね。\(+2\)ずつ増えています。
ですから、\(a=2\)になります。
次に\(b\)です。 \(x=0\) のときの \(y\) の値は \(-5\) ですから、\(b=-5\) になります。
よって、
\(y=2x-5\)
になります。
例3の答え
同様に、表から \(a\) と \(b\) を読み取ります。
今度は、\(a\) が \(3\)ずつ減っていくのが分かりますね。
\(3\)ずつ減っていくということは、\(-3\)ずつ増えてくと同じことなので、
\(a=-3\) になります。
\(b\) は表から\(4\)と読み取れるので、\(b=4\)になります。
よって答えは、
\(y=-3x+4\)
です。
最後にちょっとした応用問題をやってみましょう。
応用例題
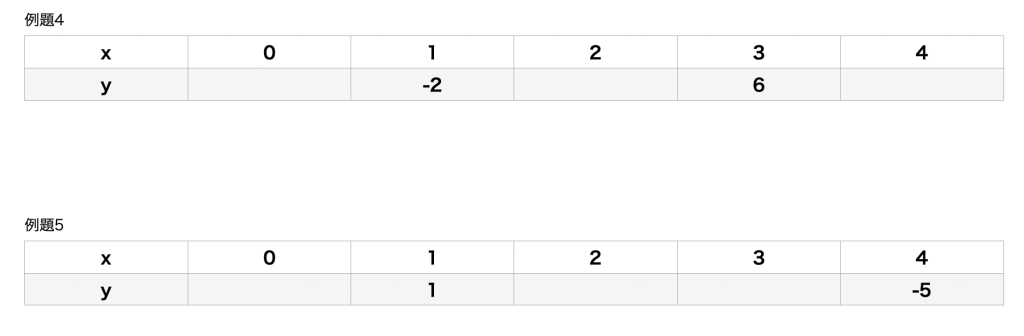
例題4答え
まずは\(a\) から求めます。
\(y\) の値がわかっているのは \(x=1\) のときと \(x=3\) なので、ここから \(x\) の増加量と\(y\) の増加量を求めます。
\(x\) の増加量は \(3-1=2\) ですね。
\(y\) の増加量は \(6-(-2)=8\) になりますね。
よって、変化の割合は
で求められるので、\(a=(8 \div 2) =4\) になります。
次に\(b\) ですが、切片は\(x=0\) のときの \(y\) の値ですが、今回は空欄なので計算して求めることになります。
変化の割合が \(4\) ですから、\(x\) が\(1\) 増えると \(y\) は \(4\)ずつ増えていきます。
\(x=1\) のとき \(y=-2\) なので、\(x=0\) のときは\(-2\) よりも\(4\)小さい値になることが分かります。
よって、\(-2-4=-6\) になります。
\(a=4\) , \(b=-6\) になるので、答は、
\(y=4x-6\)
になります。
例題5の答え
例題4と同じように考えます。
今度は \(y\) の値がわかっているのは \(x=1\) のときと \(x=4\) なので、ここから \(x\) の増加量と\(y\) の増加量を求めます。
\(x\) の増加量は \(4-1=3\) 、\(y\) の増加量は \(-5-1=-6\) になりますね。
よって、変化の割合は \(a=(-6 \div 3 )=-2\) と求めることができます。
次に \(b\) です。切片は\(x=0\) のときの \(y\) の値でしたね。
\(x=1\) のとき \(y=1\) なので、\(x=0\) のときは\(1\) よりも\(-2\)小さい値になることが分かります。
\(-2\)小さいと言うことは、\(+2\)大きいことになります。よって、\(1+2=3\) になります。
\(a=-2\),\(b=3\)になるので、答えは、
\(y=-2x+3\)
です。
表から一次関数の式を求める まとめ
表から一次関数の式の求め方は、以下の流れになります。
- 一次関数の意味をイメージしながら理解する
- 変化の割合と切片の意味を理解する
- 練習
また、「値」と「増加量」の違いをしっかり区別するように意識しましょう。
理解できたら、学校のワークや教科書の例題などで練習してみてください。
きっとこの記事を読む前よりも、スラスラ解けているはずです。
